
某企业主要生产甲、乙两种品牌的空调,由于受到空调在保修期内维修费等因素的影响,企业生产每台空调的利润与该空调首次出现故障的时间有关,甲、乙两种品牌空调的保修期均为3年,现从该厂已售出的两种品牌空调中各随机抽取50台,统计数据如下:
| 品牌 | 甲 | 乙 | |||||
| 首次出现故障时间 x年 |  |  |  |  |  |  |  |
| 空调数量(台) | 1 | 2 | 4 | 43 | 2 | 3 | 45 |
| 每台利润(千元) | 1 | 2 | 2.5 | 2.7 | 1.5 | 2.6 | 2.8 |
(1)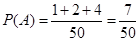 ;(2)分布列见解析;(3)生产乙品牌空调;
;(2)分布列见解析;(3)生产乙品牌空调;
解析试题分析:(1)用古典概型公式可求出概率,随机抽一台共有50种情况,在保修期3年内的共有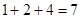 种,所以概率为
种,所以概率为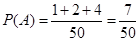 ;(2)
;(2)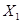 取1、2、2.5、2.7分别求出各自的概率即可,
取1、2、2.5、2.7分别求出各自的概率即可,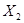 取1.5、2.6、2.8分别求出各自的概率即可;(3)求出两种空调利润的期望,哪个的期望大即选择生产那种空调。
取1.5、2.6、2.8分别求出各自的概率即可;(3)求出两种空调利润的期望,哪个的期望大即选择生产那种空调。
试题解析:解:(1)设“甲品牌空调首次出现故障发生在保修期内”为事件A,
则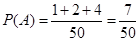 。 4分
。 4分
(2)依题意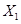 的分布列如下:
的分布列如下: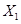
1 2 2.5 2.7 P 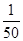
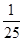
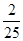
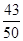
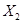 的分布列如下:
的分布列如下:
9分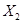
1.5 2.6 2.8 P 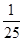
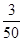
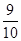
(3)由(2)得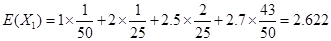 (千元); 11分
(千元); 11分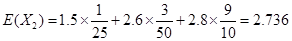 (千元)。 12分
(千元)。 12分
所以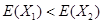 ,
,
故应生产乙品牌空调。 13分
考点:1、离散型随机变量的分布列;2、离散型随机变量的期望;


科目:高中数学 来源: 题型:解答题
红队队员甲、乙与蓝队队员A、B进行围棋比赛,甲对A、乙对B各比一盘.已知甲胜A,乙胜B的概率分别为0.6、0.5.假设各盘比赛结果相互独立.
(1)求红队至少一名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过1小时收费6元,超过1小时的部分每小时收费8元(不足1小时按1小时计算).现有甲、乙两人在该场地停车,两人停车都不超过4小时.
(Ⅰ)若甲停车1小时以上且不超过2小时的概率为 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;
(Ⅱ)若甲、乙两人每人停车的时长在每个时段的可能性相同,求甲乙二人停车付费之和为28元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
吸烟的危害很多,吸烟产生的烟雾中有近2000种有害物质,如尼古丁、氰氢酸、氨、一氧化碳、二氧化碳、吡啶、砷、铜、铅等,还有40多种致癌物,如苯并芘、朕苯胺及煤焦油等。它们随吸烟者吞咽烟雾时进入体内,对机体产生危害。为了解某市心肺疾病是否与吸烟有关,某医院随机对入院的50人进行了问卷调查,得到了如下的列联表.
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 吸烟患者 | 20 | 5 | 25 |
| 不吸烟患者 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
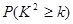 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
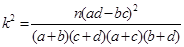 ,其中
,其中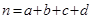
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
两人约定在20:00到21:00之间相见,并且先到者必须等迟到者40分钟方可离去,如果两人出发是各自独立的,在20:00到21:00各时刻相见的可能性是相等的,求两人在约定时间内相见的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设有关于x的一元二次方程x2+2ax+b2="0." (l)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率;(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
甲、乙两队各有n个队员,已知甲队的每个队员分别与乙队的每个队员各握手一次 (同队的队员之间不握手),从这n2次的握手中任意取两次.记事件A:两次握手中恰有3个队员参与.若事件A发生的概率P<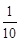 ,则n的最小值是_____________.
,则n的最小值是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com