练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验，得到5组数据，，，，．根据收集到的数据可知++++=150，由最小二乘法求得回归直线方程为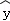=0.67x+54.9，则++++的值为（ ）

    A．75 B．155.4 C．375 D．466.2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015-2016学年湖南省、四中高二上期末文科数学试卷（解析版） 题型：填空题

    有下列命题：

    ①双曲线与椭圆有相同的焦点；

    ②；

    ③；

    ④；

    ⑤，．

    其中正确命题的序号为____________．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年北京市怀柔区高一上期末数学试卷（解析版） 题型：解答题

    已知，且．

    （Ⅰ）求的值；

    （Ⅱ）求的值．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年黑龙江省高二下期中文科数学试卷（解析版） 题型：解答题

    在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系.已知曲线C：，过点P（﹣2，﹣4）的直线l的参数方程为.l与C分别交于点M、N．

    （1）写出曲线C和直线 l的普通方程；

    （2）若|PM|，|MN|，|PN|成等比数列，求a的值．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年黑龙江省高二下期中文科数学试卷（解析版） 题型：填空题

    设则函数是增函数的概率为 .

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年黑龙江省高二下期中文科数学试卷（解析版） 题型：选择题

    在如图所示的茎叶图中，甲、乙两组数据的中位数分别是 （ ）

    A．45和47 B．45 和44 C．45和42 D．45和45

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年黑龙江省高二下期中理科数学试卷（解析版） 题型：解答题

    某商场销售某种品牌的空调器，每周周初购进一定数量的空调器，商场每销售一台空调器可获利500元，若供大于求，则每台多余的空调器需交保管费100元；若供不应求，则可从其他商店调剂供应，此时每台空调器仅获利润200元。

    （Ⅰ）若该商场周初购进20台空调器，求当周的利润（单位：元）关于当周需求量n（单位：台，）的函数解析式；

    （Ⅱ）该商场记录了去年夏天（共10周）空调器需求量n（单位：台），整理得下表：

    周需求量n

    18

    19

    20

    21

    22

    频数

    1

    2

    3

    3

    1

    以10周记录的各需求量的频率作为各需求量发生的概率，若商场周初购进20台空调器，X表示当周的利润（单位：元），求X的分布列及数学期望。

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年黑龙江省高二下期中理科数学试卷（解析版） 题型：选择题

    已知，其中是实数，i是虚数单位，则=（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年福建省高二下期中理科数学试卷（解析版） 题型：选择题

    已知函数，，若恒成立，则实数的取值范围是（ ）

    A． B． C． D．

    查看答案和解析>>

    同步练习册答案