天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2016届安徽省高三下组卷三理科数学试卷（解析版） 题型：填空题
公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出
的值为____________．（参考数据：
）
查看答案和解析>>
科目：高中数学 来源：2016届福建省高三最后一卷文科数学试卷（解析版） 题型：解答题
去年年底，某商业集团公司根据相关评分细则，对其所属25家商业连锁店进行了考核评估．将各连锁店的评估分数按
分成四组，其频率分布直方图如下图所示，集团公司依据评估得分，将这些连锁店划分为
四个等级，等级评定标准如下表所示．
（1）估计该商业集团各连锁店评估得分的众数和平均数；
（2）从评估分数不小于80分的连锁店中任选2家介绍营销经验，求至少选一家
等级的概率．
查看答案和解析>>
科目：高中数学 来源：2016届福建省高三最后一卷理科数学试卷（解析版） 题型：解答题
为评估设备
生产某种零件的性能，从设备生产零件的流水线上随机抽取100件零件做为样本，测量其直径后，整理得到下表：
经计算，样本的平均值
，标准差
，以频率值作为概率的估计值．
（I）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为
，并根据以下不等式进行评判（
表示相应事件的频率）；
①
；②
；
③
．评判规则为：若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙，若仅满足其中一个，则等级为丙；若全部不满足，则等级为丁．试判断设备的性能等级．
（II）将直径小于等于
或直径大于
的零件认为是次品
（ⅰ）从设备的生产流水线上随意抽取2件零件，计算其中次品个数
的数学期望
；
（ⅱ）从样本中随意抽取2件零件，计算其中次品个数
的数学期望
．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年河北省高二下期中文科数学试卷（解析版） 题型：选择题
已知变量
的取值如下表
| 0 | 1 | 3 | 4 |
| 2.2 | 4.3 | 4.8 | 6.7 |
利用散点图观察，
与
线性相关，其回归方程为
，则
的值为（ ）
A．
B．
C．
D． 
查看答案和解析>>
科目：高中数学 来源：2015-2016学年山西大学附属中学高一下期中数学试卷（解析版） 题型：选择题
设
为基底向量,已知向量
,若
三点共线,则实数
的值等于（ ）
A. 
B. 
C. 
D.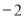 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
为单位向量，向量
，且
，则向量
的夹角为______．
，
，则
中元素的个数是（ ）
满足约束条件
，若
仅在点
处取得最大值，则
的值可以为（ ）
D．
，
，则
等于（ ）
B．
D．