
(本小题满分12分)
已知函数
(1)若
(2)若函数 的图像上有与
的图像上有与 轴平行的切线,求
轴平行的切线,求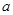 的取值范围。
的取值范围。
(3)若函数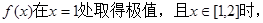

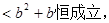 求
求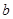 的取值范围。
的取值范围。
(1)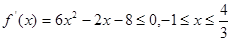 ;(2)由
;(2)由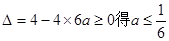 ;
;
(3)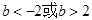 。
。
解析试题分析: (1)先求解导数,然后利用导数大于零得到单调增区间
(2)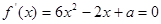
依题意,知方程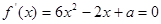 有实根,结合判别式得到大于等于零,求得范围。
有实根,结合判别式得到大于等于零,求得范围。
(3)利用函数在x=1处取得极值,进而分析求解得到参数a的值,再得到另一个极值点进而分析得到最值证明不等式。
(1)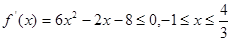 ……………………2分
……………………2分
(2)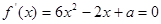
依题意,知方程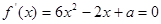 有实根……………4分
有实根……………4分
所以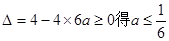 ……………6分
……………6分
(3)由函数 在
在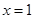 处取得极值,知
处取得极值,知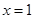 是方程
是方程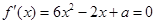
的一个根,所以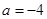 , ┄┄┄┄┄┄┄┄┄7分
, ┄┄┄┄┄┄┄┄┄7分
方程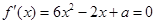 的另一个根为
的另一个根为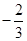
因此,当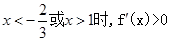 ,当
,当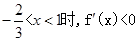
所以,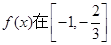 和
和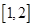 上为增函数,在
上为增函数,在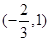 上为减函数,
上为减函数,
因此,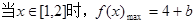 ┄┄┄┄┄┄11分
┄┄┄┄┄┄11分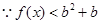 恒成立,
恒成立,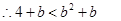
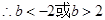 ┄┄┄┄┄12分
┄┄┄┄┄12分
考点:本题主要考查了导数在研究函数中的运用。研究函数单调性和函数的极值问题,以及函数的最值的求解。
点评:解决该试题的关键是求解导数,分析导数的正负对于函数单调性的影响,以及导数的几何意义求解切线方程问题中两个要素:切点和切线的斜率。


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有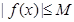 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的上界.
的上界.
(1)判断函数 是否是有界函数,请写出详细判断过程;
是否是有界函数,请写出详细判断过程;
(2)试证明:设 ,若
,若 在
在 上分别以
上分别以 为上界,
为上界,
求证:函数 在
在 上以
上以 为上界;
为上界;
(3)若函数 在
在 上是以3为上界的有界函数,
上是以3为上界的有界函数,
求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小王需不定期地在某超市购买同一品种的大米.现有甲、乙两种不同的采购策略,策略甲:每次购买大米的数量一定;策略乙:每次购买大米的钱数一定.若以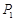 (元)和
(元)和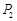 (元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
(元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数f(x)=x2+(2+lga)x+lgb,f(-1)=-2.
(1)求a与b的关系式;
(2)若f(x)≥2x恒成立,求a、b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某工厂修建一个长方体无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的 造价为150元,池壁每平方米的造价为120元.设池底长方形长为 米.
米.
(1)求底面积,并用含 的表达式表示池壁面积;
的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
设函数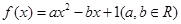 ,
,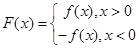
(1) 如果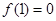 且对任意实数
且对任意实数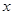 均有
均有 ,求
,求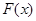 的解析式;
的解析式;
(2) 在(1)在条件下, 若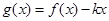 在区间
在区间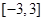 是单调函数,求实数
是单调函数,求实数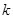 的取值范围;
的取值范围;
(3) 已知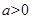 且
且 为偶函数,如果
为偶函数,如果 ,求证:
,求证: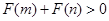 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.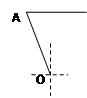
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行时间应为多少小时?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com