
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)对函数![]() 求导,根据
求导,根据![]() 讨论
讨论![]() 的取值及
的取值及![]() 的单调性,从而得到函数的极值;
的单调性,从而得到函数的极值;
(Ⅱ)根据当![]() 时,
时,![]() 恒成立,转化为
恒成立,转化为![]() 恒成立,再构造函数
恒成立,再构造函数![]()
![]() ,利用导数及函数的单调性讨论
,利用导数及函数的单调性讨论![]() 的范围求最值得到答案.
的范围求最值得到答案.
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增,则函数
上单调递增,则函数![]() 无极值;
无极值;
当![]() 时,令
时,令![]() ,则
,则![]() ,
,
故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
从而![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 取得极小值
取得极小值![]() ,无极大值;
,无极大值;
综上可知,当![]() 时,函数
时,函数![]() 无极值;
无极值;
当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(Ⅱ)当![]() ,
,![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
即![]() 恒成立,令
恒成立,令![]() ,
,
则![]() 恒成立,即
恒成立,即![]() ,
,
则必有![]() 成立,即
成立,即![]() .
.
![]() ,
,
令![]() ,则
,则![]() ,可知
,可知![]() ,
,
由![]() 知,当
知,当![]() 时,
时,![]() ,
,
可知![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]()
![]() ,
,
所以只需![]() ,即
,即![]() ,故
,故![]() ;
;
当![]() 时,
时,![]() ,可知
,可知![]() )时,
)时,![]() ,
,
![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,只需
,只需![]() ,
,
即![]() 成立,即
成立,即![]() .
.
综上可知,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】若存在实数k,b,使得函数![]() 和
和![]() 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足:![]() 且
且![]() ,则称直线:
,则称直线:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中e为自然对数的底数).试问:
(其中e为自然对数的底数).试问:
(1)函数![]() 和
和![]() 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与直线
与直线![]() 分别与椭圆
分别与椭圆![]()
![]() 交于点
交于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,是否存在经过原点,且以
两点,是否存在经过原点,且以![]() 为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
为直径的圆?若有,请求出圆的方程,若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点坐标是
的两个顶点坐标是![]() ,
,![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 是坐标原点,点
是坐标原点,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若互相平行的两条直线![]() ,
,![]() 分别过定点
分别过定点![]() 和
和![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第3次停止摸球的概率,利用计算机软件产生随机数,每1组中有3个数字,分别表示每次摸球的结果,经随机模拟产生了以下18组随机数:
131 432 123 233 234 122 332 141 312 241 122 214 431 241 141 433 223 442
由此可以估计恰好在第3次停止摸球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
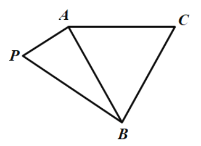
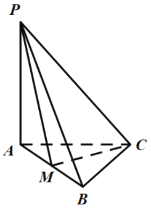
【题目】如图所示,平面四边形![]() 中,
中,![]() 为直角,
为直角,![]() 为等边三角形,现把
为等边三角形,现把![]() 沿着
沿着![]() 折起,使得平面
折起,使得平面![]() 与平面
与平面![]() 垂直,且点M为
垂直,且点M为![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算几何体体积的祖暅原理:“幂势既同,则积不容异“.意思是两个同高的几何体,如果在等高处的截面积都相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为3的圆的三分之一,则该几何体的体积为( )
A.![]() πB.
πB.![]() πC.4
πC.4![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是2020项的实数数列,
是2020项的实数数列,![]() 中的每一项都不为零,
中的每一项都不为零,![]() 中任意连续11项
中任意连续11项![]() 的乘积是定值
的乘积是定值![]() .
.
①存在满足条件的数列,使得其中恰有365个1;
②不存在满足条件的数列,使得其中恰有550个1.
命题的真假情况为( )
A.①和②都是真命题B.①是真命题,②是假命题
C.②是真命题,①是假命题D.①和②都是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com