Question

【题目】已知直线PA，PB分别与半径为1的圆O相切于点A，B，PO=2， ．若点M在圆O的内部（不包括边界），则实数λ的取值范围是（ ）
A.（﹣1，1）
B.
C.
D.（0，1）

Answer 1

【答案】B
【解析】解法一：如图，在线段PA的延长线上取点Q，使得PA=AQ，连接OQ，交圆于C， 由圆的半径为1，PO=2可得∠BOP=∠AOP=∠AOQ=60°，PB= ，故B，O，Q三点共线，且BQ=3
因为2 = ，∴ =λ +（1﹣λ） ． ．
由点M在圆O的内部（不包括边界），∴0＜
故选：B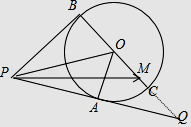

解法二：以O为原点， 的方向为x轴正方向建立平面直角坐标系，则P（2，0）
A（ ），B（ ，﹣ ），设M（x0 ， y0），
由 ．得 ，y0= ，
∵M（x0 ， y0）在圆O的内部（不包括边界），∴ ，
整理得﹣1＜3λ﹣1＜1，解得0＜
故选：B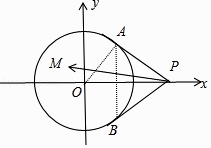

【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使才能正确解答此题．