
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若存在![]() 及唯一正整数
及唯一正整数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(2)
;(2) ![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:
(1)求出函数![]() 的导函数,通过对导函数符号的讨论可得函数的单调性.(2)由题意得函数
的导函数,通过对导函数符号的讨论可得函数的单调性.(2)由题意得函数![]() 在
在![]() 上的值域为
上的值域为![]() .结合题意可将问题转化为当
.结合题意可将问题转化为当![]() 时,满足
时,满足![]() 的正整数解只有1个.通过讨论
的正整数解只有1个.通过讨论![]() 的单调性可得只需满足
的单调性可得只需满足 ,由此可得所求范围.
,由此可得所求范围.
试题解析:
(1)由题意知函数的定义域为![]() .
.
因为![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时, ![]() 是增函数,
是增函数,
又![]() ,
,
故当![]() 时,
时, ![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() 单调递增.
单调递增.
所以![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知当![]() 时,
时, ![]() 取得最小值,
取得最小值,
又![]() ,
,
所以![]() 在
在![]() 上的值域为
上的值域为![]() .
.
因为存在![]() 及唯一正整数
及唯一正整数![]() ,使得
,使得![]() ,
,
所以满足![]() 的正整数解只有1个.
的正整数解只有1个.
因为![]() ,
,
所以![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以 ,即
,即 ,
,
解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线PA,PB分别与半径为1的圆O相切于点A,B,PO=2, ![]() .若点M在圆O的内部(不包括边界),则实数λ的取值范围是( )
.若点M在圆O的内部(不包括边界),则实数λ的取值范围是( )
A.(﹣1,1)
B.![]()
C.![]()
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是 ( )
①相关系数![]() 用来衡量两个变量之间线性关系的强弱,
用来衡量两个变量之间线性关系的强弱, ![]() 越接近于
越接近于![]() ,相关性越弱;
,相关性越弱;
②回归直线![]() 一定经过样本点的中心
一定经过样本点的中心![]() ;
;
③随机误差![]() 满足
满足![]() ,其方差
,其方差![]() 的大小用来衡量预报的精确度;
的大小用来衡量预报的精确度;
④相关指数![]() 用来刻画回归的效果,
用来刻画回归的效果, ![]() 越小,说明模型的拟合效果越好.
越小,说明模型的拟合效果越好.
A. ①② B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,第二十一届世界杯足球赛将在俄罗斯拉开帷幕.为了了解喜爱足球运动是否与性别有关,某体育台随机抽取100名观众进行统计,得到如下![]() 列联表.
列联表.

(1)将![]() 列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜爱足球运动与性别有关?
列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜爱足球运动与性别有关?
(2)在不喜爱足球运动的观众中,按性别分别用分层抽样的方式抽取6人,再从这6人中随机抽取2人参加一台访谈节目,求这2人至少有一位男性的概率.
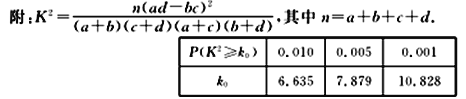
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,过右焦点F2(c,0)垂直于x轴的直线与椭圆交于A,B两点且|AB|=
,过右焦点F2(c,0)垂直于x轴的直线与椭圆交于A,B两点且|AB|= ![]() ,又过左焦点F1(﹣c,0)任作直线l交椭圆于点M
,又过左焦点F1(﹣c,0)任作直线l交椭圆于点M
(1)求椭圆C的方程
(2)椭圆C上两点A,B关于直线l对称,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知倾斜角为135°且过点P(1,2)的直线l与曲线C交于M,N两点,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com