
【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ![]() ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 ![]() <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号)
【答案】②③
【解析】解:①若x=3,y=1,则f2(x)﹣f2(y)=1﹣1=0,f(x+y)f(x﹣y)=f(4)f(2)=1,不满足集合条件,故f(x)M,故①错误;
②由f(x)=2x得:f2(x)﹣f2(y)=4x2﹣4y2 , f(x+y)f(x﹣y)=2(x+y)2(x﹣y)=4x2﹣4y2 , 满足等式,故f(x)∈M,故②正确;
③由题意知,函数f(x)满足f2(x)﹣f2(y)=f(x+y)f(x﹣y),令x=y=0得:f(0)=0;再令x=0得:﹣f2(y)=f(y)f(﹣y),即有f(y)[f(y)+f(﹣y)]=0,所以f(y)=0或f(﹣y)=﹣f(y),当f(y)=0时,函数图象关于原点对称,当f(﹣y)=﹣f(y)时,函数为奇函数,图象也关于原点对称,故③正确;④取f(x)=﹣x,因为f2(x)﹣f2(y)=x2﹣y2 , f(x+y)f(x﹣y)=﹣(x+y)(y﹣x)=x2﹣y2 , 所以f(x)∈M,而f(x)=﹣x为减函数,故④错误.
综上可得:②③正确.
所以答案是:②③.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 分别是
分别是![]() 中点,弧
中点,弧![]() 的半径分别为
的半径分别为![]() ,点
,点![]() 平分弧
平分弧![]() ,过点
,过点![]() 作弧
作弧![]() 的切线分别交
的切线分别交![]() 于点
于点![]() .四边形
.四边形![]() 为矩形,其中点
为矩形,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在弧
在弧![]() 上,延长
上,延长![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() .
.
(1)求![]() 的解析式并求其定义域;
的解析式并求其定义域;
(2)求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a是实数,f(x)=a﹣ ![]() (x∈R).
(x∈R).
(1)证明不论a为何实数,f(x)均为增函数;
(2)若f(x)满足f(﹣x)+f(x)=0,解关于x的不等式f(x+1)+f(1﹣2x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( ) 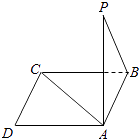
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,
, ![]() 是平面上一点,若存在过点
是平面上一点,若存在过点![]() 的直线与
的直线与![]() 都有公共点,则称
都有公共点,则称![]() 为“
为“![]() 型点”.
型点”.

(1)证明: ![]() 的左焦点是“
的左焦点是“![]() 型点”;
型点”;
(2)设直线![]() 与
与![]() 有公共点,求证:
有公共点,求证: ![]() ,进而证明原点不是“
,进而证明原点不是“![]() 型点”;
型点”;
(3)求证: ![]() 内的点都不是“
内的点都不是“![]() 型点”.
型点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发出一款产品,批量生产前先在某城市销售30天进行市场调查.调查结果发现:日销量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系:每件产品的销售利润
的对应关系服从图①所示的函数关系:每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系.图①由抛物线的一部分(
的对应关系服从图②所示的函数关系.图①由抛物线的一部分(![]() 为抛物线顶点)和线段
为抛物线顶点)和线段![]() 组成.
组成.
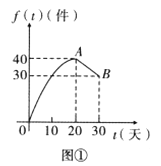
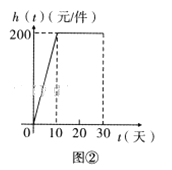
(Ⅰ)设该产品的日销售利润![]()
![]() ,分别求出
,分别求出![]() ,
, ![]() ,
, ![]() 的解析式,
的解析式,
(Ⅱ)若在30天的销售中,日销售利润至少有一天超过8500元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com