
 的取值范围.
的取值范围. =
= ,再由二次函数的性质求得
,再由二次函数的性质求得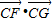 的最大值和最小值,
的最大值和最小值,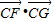 的取值范围.
的取值范围. ,解之得:
,解之得: ,∴A(-2,-8),
,∴A(-2,-8), ,即 7x-6y-34=0.
,即 7x-6y-34=0. 解得
解得 ,即C(4,-1),又 圆心M(0,-1),
,即C(4,-1),又 圆心M(0,-1), =
= =(16-r2)cos2∠CFM=(16-r2)(1-2sin2∠GCM)=
=(16-r2)cos2∠CFM=(16-r2)(1-2sin2∠GCM)= ,
, =
= ,
, =
= .
. 的取值范围为
的取值范围为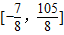 .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| CF |
| CG |
查看答案和解析>>
科目:高中数学 来源:设计选修数学-1-1苏教版 苏教版 题型:044
在△ABC中,点B(-6,0)、C(0,8),且sinB,sinA,sinC成等差数列.
(1)求证:顶点A在一个椭圆上运动.
(2)指出这个椭圆的焦点坐标以及焦距.
查看答案和解析>>
科目:高中数学 来源:选修设计数学1-1北师大版 北师大版 题型:044
在△ABC中,点B(-6,0)、C(0,8),且sinB、sinA、sinC成等差数列.
(1)求证:顶点A在一个椭圆上运动.
(2)指出这个椭圆的焦点坐标以及焦距.
查看答案和解析>>
科目:高中数学 来源:江苏期中题 题型:解答题
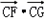 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com