
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM,并写出x的取值范围;
(2)求S关于x的函数关系式.
科目:高中数学 来源: 题型:解答题
已知二次函数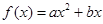 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为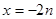 ,
,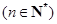 .
.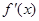 是
是 的导函数,且
的导函数,且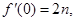
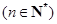 .
.
(1)求 的表达式(含有字母
的表达式(含有字母 );
);
(2)若数列 满足
满足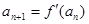 ,且
,且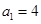 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在(2)条件下,若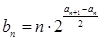 ,
,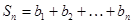 ,是否存在自然数
,是否存在自然数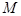 ,使得当
,使得当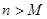 时
时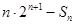
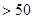 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的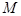 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x吨、3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某种细胞分裂时,由于在分裂过程 中,有些细胞会自动消亡,分裂次数
中,有些细胞会自动消亡,分裂次数 与第
与第 次得到的细胞总数
次得到的细胞总数 近似的满足关系
近似的满足关系
 ,则由
,则由 个细胞分裂达到
个细胞分裂达到 个细胞所需的分裂次数至少是_____次.(
个细胞所需的分裂次数至少是_____次.( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com