
设函数 定义域为
定义域为 .
.
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(1)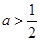 ,(2)
,(2)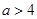 .
.
解析试题分析:(1)因为 ,所以
,所以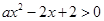 在
在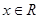 上恒成立. ① 当
上恒成立. ① 当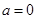 时,由
时,由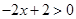 ,得
,得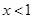 ,不成立,舍去,② 当
,不成立,舍去,② 当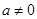 时,由
时,由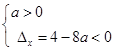 ,得
,得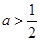 ,综上所述,实数
,综上所述,实数 的取值范围是
的取值范围是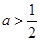 .(2))恒成立问题一般利用变量分离法转化为最值问题. 依题有
.(2))恒成立问题一般利用变量分离法转化为最值问题. 依题有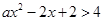 在
在 上恒成立,所以
上恒成立,所以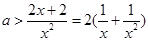 在
在 上恒成立, 令
上恒成立, 令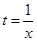 ,则由
,则由 ,得
,得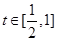 ,记
,记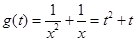 ,由于
,由于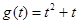 在
在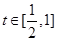 上单调递增, 所以
上单调递增, 所以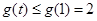 ,
, 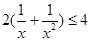
因此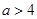
试题解析:解:(1)因为 ,所以
,所以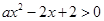 在
在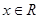 上恒成立. 2分
上恒成立. 2分
① 当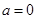 时,由
时,由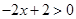 ,得
,得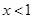 ,不成立,舍去, 4分
,不成立,舍去, 4分
② 当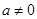 时,由
时,由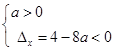 ,得
,得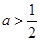 , 6分
, 6分
综上所述,实数 的取值范围是
的取值范围是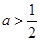 . 8分
. 8分
(2)依题有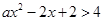 在
在 上恒成立, 10分
上恒成立, 10分
所以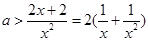 在
在 上恒成立, 12分
上恒成立, 12分
令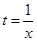 ,则由
,则由 ,得
,得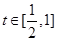 ,
,
记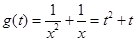 ,由于
,由于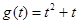 在
在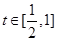 上单调递增,
上单调递增,
所以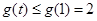 ,
, 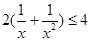
因此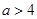 16分
16分
(使用函数在定义区间上最小值大于0求解可参照给分)
考点:不等式恒成立问题


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM,并写出x的取值范围;
(2)求S关于x的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数 与时刻
与时刻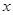 (时)的关系为
(时)的关系为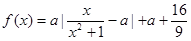 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且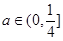 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作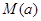 .
.
(1)令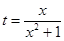 ,
, ,求
,求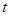 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元.
(1)试将 表示成
表示成 的函数;
的函数;
(2)需要修建多少个增压站才能使 最小,其最小值为多少?
最小,其最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果n件产品中任取一件样品是次品的概率为 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
).
(1)求该企业日赢利额 的最大值;
的最大值;
(2)为保证每天的赢利额不少于日赢利额最大值的50%,试求该企业日产量的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
请你设计一个包装盒,如图所示, 是边长为
是边长为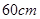 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.
(1)若广告商要求包装盒侧面积 最大,试问
最大,试问 应取何值?
应取何值?
(2)若广告商要求包装盒容积 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
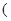 常数
常数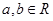 )满足
)满足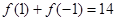 .
.
(1)求出 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;
(2)若 在区间
在区间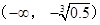 上单调递减,求
上单调递减,求 的最小值;
的最小值;
(3)在(2)的条件下,当 取最小值时,证明:
取最小值时,证明: 恰有一个零点
恰有一个零点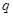 且存在递增的正整数数列
且存在递增的正整数数列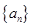 ,使得
,使得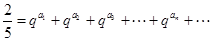 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com