
分析 先求出圆H的方程,再根据直线l过点C,且被⊙H截得的弦长为2,设出直线方程,利用勾股定理,即可求直线l的方程
解答 解:线段AB的垂直平分线方程为x=0,线段BC的垂直平分线方程为x+y-3=0,
所以外接圆圆心为H(0,3),半径为$\sqrt{{1^2}+{3^2}}=\sqrt{10}$,
故⊙H的方程为x2+(y-3)2=10.
设圆心H到直线l的距离为d,
因为直线l被⊙H截得的弦长为2,所以$d=\sqrt{{{(\sqrt{10})}^2}-1}=3$.
当直线l垂直于x轴时,显然符合题意,即x=3为所求;
当直线l不垂直于x轴时,设直线方程为y-2=k(x-3),则$\frac{|-3k-1|}{{\sqrt{1+{k^2}}}}=3$,解得$k=\frac{4}{3}$.
综上,直线l的方程为x=3或4x-3y-6=0.
点评 本题考查圆的方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意待定系数法及点到直线的公式的合理运用.


科目:高中数学 来源: 题型:解答题
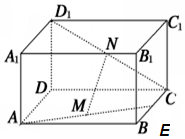 如图,已知长方体ABCD-A1B1C1D1中,E、M、N分别是BC、AE、CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1.
如图,已知长方体ABCD-A1B1C1D1中,E、M、N分别是BC、AE、CD1的中点,AD=AA1=a,AB=2a.求证:MN∥平面ADD1A1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=log2|x| | B. | y=3-x | C. | y=$\frac{1}{x}$ | D. | y=-x2+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com