
如图,在直三棱柱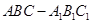 中,D、E分别是BC和
中,D、E分别是BC和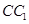 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.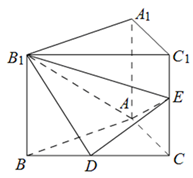
(1)求证: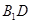 ⊥平面
⊥平面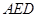 ;
;
(2)求二面角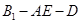 的余弦值;
的余弦值;
(3)求三棱锥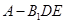 的体积.
的体积.
(1)见解析 (2)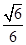 (3)8
(3)8
解析试题分析:
(1)(2)(3)均可利用坐标法,即分别以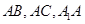 建立三维空间坐标系.下面重点分析法2
建立三维空间坐标系.下面重点分析法2
(1)利用勾股定理可以求的线段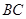 的长,而要证明
的长,而要证明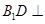 面
面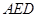 ,只需要证明
,只需要证明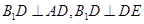 ,首先可以三次利用勾股定理把
,首先可以三次利用勾股定理把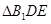 的三条边长求出,再利用勾股定理证明
的三条边长求出,再利用勾股定理证明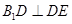 ,线段
,线段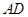 为等腰直角三角形ABC的三线合一即有
为等腰直角三角形ABC的三线合一即有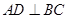 ,可得到
,可得到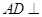 面
面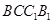 ,进而得到
,进而得到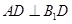 ,即可通过线线垂直证明
,即可通过线线垂直证明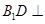 面DAE.
面DAE.
(2)要求二面角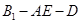 的余弦值,需要作出该二面角的平面角,为此过D做DM⊥AE于点M,连接B1M.,根据第一问有
的余弦值,需要作出该二面角的平面角,为此过D做DM⊥AE于点M,连接B1M.,根据第一问有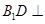 面AED且
面AED且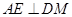 可以得到
可以得到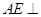 面
面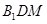 ,则
,则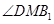 即为所求二面角的平面角,即该角的余弦值为
即为所求二面角的平面角,即该角的余弦值为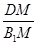 .利用勾股定理即可得到
.利用勾股定理即可得到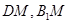 的长,进而得到二面角的余弦值.
的长,进而得到二面角的余弦值.
(3)由(1)可得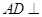 面
面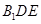 ,则该三棱锥可以以
,则该三棱锥可以以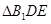 作为底面,高为
作为底面,高为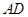 来求的体积,而AD和三角形的面积都可以用勾股定理求的.
来求的体积,而AD和三角形的面积都可以用勾股定理求的.
试题解析: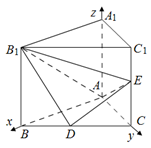
法1:依题意,建立如图所示的空间直角坐标系A-xyz.因为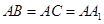 =4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分)
=4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分)
(1)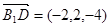 ,
,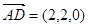 ,
,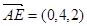 . (2分)
. (2分)
因为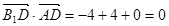 ,所以
,所以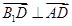 ,即
,即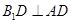 . (3分)
. (3分)
因为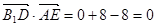 ,所以
,所以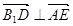 ,即
,即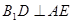 . (4分)
. (4分)
又AD、AEÌ平面AED,且AD∩AE=A,故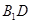 ⊥平面
⊥平面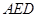 . (5分)
. (5分)
(2)由(1)知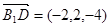 为平面AED的一个法向量. (6分)
为平面AED的一个法向量. (6分)
设平面 B1AE的法向量为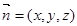 ,因为
,因为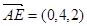 ,
,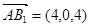 ,
,
所以由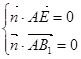 ,得
,得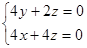 ,令y=1,得x=2,z=-2.即
,令y=1,得x=2,z=-2.即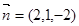 .(7分)
.(7分)
∴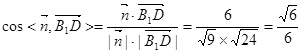 , (8分)
, (8分)
∴二面角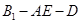 的余弦值为
的余弦值为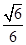 . (9分)
. (9分)
(3)由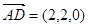 ,
,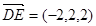 ,得
,得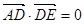 ,所以AD⊥DE. (10分)
,所以AD⊥DE. (10分)
由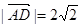 ,
, ,得
,得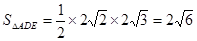 . (11分)
. (11分)
由(1)得B1D为三棱锥B1-ADE的高,且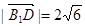 , (12分)
, (12分)
所以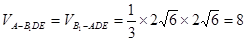


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
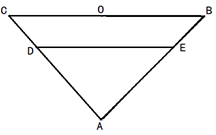
如图,在等腰直角三角形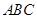 中,
中, 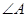 =900 ,
=900 ,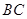 ="6,"
="6," 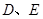 分别是
分别是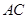 ,
,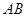 上的点,
上的点,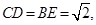
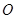 为
为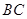 的中点.将
的中点.将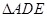 沿
沿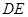 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎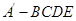 ,其中
,其中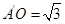
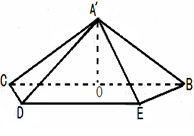
(1)证明: ;
;
(2)求二面角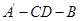 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,几何体E ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.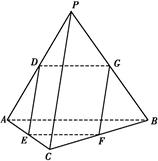
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E、G分别是棱SA、
SC的中点.求证:
(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC=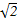 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.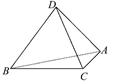
(1)当平面ADB⊥平面ABC时,求CD.
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com