
分析 (Ⅰ)利用数量积公式求出A的余弦值,进而求角A的大小;
(Ⅱ)利用余弦定理得到a,b,c三边,判断三角形的形状.
解答 解:(Ⅰ)由向量$\overrightarrow{m}$=(1,2),$\overrightarrow{n}$=(-1,cosA),且$\overrightarrow{m}•\overrightarrow{n}$=0.
得到-1+2cosA=0解得cosA=$\frac{1}{2}$,由0<A<π,所以A=$\frac{π}{3}$;
(Ⅱ)证明:在△ABC中,因为a2=b2+c2-2bccosA,且a=$\sqrt{3}$,b+c=2$\sqrt{3}$,
所以3=b2+c2-2bc$•\frac{1}{2}$=b2+c2-bc=(b+c)2-3bc,解得c=$\sqrt{3}$,所以b=$\sqrt{3}$,
所以a=b=c=$\sqrt{3}$,所以三角形为等边三角形.
点评 本题考查了平面向量的数量积运用以及利用余弦定理判断三角形的形状;属于基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
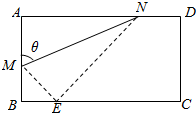 如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.
如图,折叠矩形纸片ABCD,使A点落在边BC上的E处,折痕的两端点M、N分别在线段AB和AD上(不与端点重合).已知AB=2,BC=$\frac{{4\sqrt{3}}}{3}$,设∠AMN=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c成等差数列 | B. | $\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$成等比数列 | ||
| C. | a2,b2,c2成等差数列 | D. | a2,b2,c2成等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1 | B. | y=-1 | C. | y=$\frac{1}{16}$ | D. | y=-$\frac{1}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com