
分析 (1)利用f(x)是奇函数,f(0)=0,f(-1)+f(1)=0,求出a、b的值;
(2)由(1)得f(x)定义域上的减函数,把不等式f(log${\;}_{\frac{1}{3}}$x)+f(-1)>0化为${log}_{\frac{1}{3}}$x<1,求出解集即可.
解答 解:(1)∵函数f(x)=$\frac{-{2}^{x}+a}{{2}^{x+1}-b}$是奇函数,
∴f(0)=$\frac{-1+a}{2-b}$=0,
解得a=1;
又f(-1)+f(1)=$\frac{-\frac{1}{2}+1}{1-b}$+$\frac{-2+1}{{2}^{2}-b}$=$\frac{\frac{1}{2}b+1}{(1-b)(4-b)}$=0,
解得b=-2;
(2)由(1)得,f(x)=$\frac{{-2}^{x}+1}{{2}^{x+1}+2}$=-$\frac{1}{2}$+$\frac{1}{{2}^{x}+1}$是定义域上的减函数,
∴不等式f(log${\;}_{\frac{1}{3}}$x)+f(-1)>0可化为
f(${log}_{\frac{1}{3}}$x)>-f(-1)=f(1),
即${log}_{\frac{1}{3}}$x<1,
解得x>$\frac{1}{3}$;
∴该不等式的解集为{x|x>$\frac{1}{3}$}.
点评 本题考查了不等式的解法与应用问题,也考查了函数的性质与应用问题,是综合性题目.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
 如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
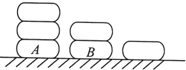 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com