
分析 (1)求解n=1时,得出a1,n≥2时,运用an=Sn-Sn-1,合并通项公式即可.
(2)所以 根据条件得出方程组$\left\{\begin{array}{l}{{b}_{1}+6d=16}\\{{b}_{1}+14d=32}\end{array}\right.$,运用求和公式求解即可.
解答 (1)因为数列{an}的前N项和Sn=2n+2-4.
所以a1=S1=23-4=4
当n>1时,an=Sn-Sn-1=(2n+2-4)-(2n+1-4)=2n+1,
因为n=1时也适合,所以an=2n+1(n∈N*);
(2)设等差数列{bn}的首项为b1,公差为d,因为b7=a3,b15=a4,an=2n+1
所以 $\left\{\begin{array}{l}{{b}_{1}+6d=16}\\{{b}_{1}+14d=32}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{b}_{1}=4}\\{d=2}\end{array}\right.$,
所以数列{bn}前n项和Tn=nb1$+\frac{n(n-1)}{2}$d=n2+3n.
点评 本题考察了数列的递推关系式的运用求解通项公式,关键是n=1别忘了,运用条件的方程组,计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
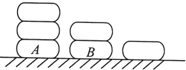 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com