
����Ŀ��������ʵ����k��b��ʹ�ú���F��x����G��x�����乫���������ϵ�����ʵ��x�����㣺F��x����kx+b��G��x����kx+b���������ƴ�ֱ��y=kx+bΪF��x����G��x���ġ�����ֱ�ߡ�����֪����f��x��=x2��x��R����g��x��= ![]() ��x��0����h��x��=2elnx�����������⣺
��x��0����h��x��=2elnx�����������⣺
��F��x��=f��x����g��x���� ![]() �ڵ���������
�ڵ���������
��f��x����g��x��֮����ڡ�����ֱ�ߡ�����b����СֵΪ��4��
��f��x����g��x��֮����ڡ�����ֱ�ߡ�����k��ȡֵ��Χ�ǣ���4��0]��
��f��x����h��x��֮�����Ψһ�ġ�����ֱ�ߡ�y=2 ![]() x��e��
x��e��
����������ĸ���Ϊ������������ȷ�������ţ�
���𰸡��٢ڢ�
���������⣺�١�F��x��=f��x����g��x��=x2�� ![]() ����x�ʣ���
����x�ʣ��� ![]() ��0����F�䣨x��=2x+
��0����F�䣨x��=2x+ ![]() ��0����F��x��=f��x����g��x����x�ʣ���
��0����F��x��=f��x����g��x����x�ʣ��� ![]() ��0���ڵ����������ʢٶԣ�
��0���ڵ����������ʢٶԣ�
�ڡ�����f��x����g��x���ĸ���ֱ��Ϊy=kx+b����x2��kx+b��һ��ʵ��x���������С�1��0��k2+4b��0��
�� ![]() ��kx+b��һ��x��0��������kx2+bx��1��0������2��0��b2+4k��0��k��0��b��0��
��kx+b��һ��x��0��������kx2+bx��1��0������2��0��b2+4k��0��k��0��b��0��
����k2�ܩ�4b��b2�ܩ�4k��k4��16b2�ܩ�64k��4��k��0��ͬ����4��b��0���ʢڶԣ��۴���
�ܺ���f��x����h��x����ͼ����x= ![]() ���й����㣬��˴���f��x����g��x���ĸ���ֱ�ߣ�
���й����㣬��˴���f��x����g��x���ĸ���ֱ�ߣ�
��ô��ֱ�߹���������㣬�����ֱ�ߵ�б��Ϊk�������ֱ�߷���Ϊy��e=k��x�� ![]() ������y=kx��k
������y=kx��k ![]() +e��
+e��
��f��x����kx��k ![]() +e��x��R�����ɵ�x2��kx+k
+e��x��R�����ɵ�x2��kx+k ![]() ��e��0��x��R�������
��e��0��x��R�������
�����0��ֻ��k=2 ![]() ����ʱֱ�߷���Ϊ��y=2
����ʱֱ�߷���Ϊ��y=2 ![]() x��e��
x��e��
����֤��h��x����2 ![]() x��e����G��x��=2
x��e����G��x��=2 ![]() x��e��h��x��=2
x��e��h��x��=2 ![]() x��e��2elnx��
x��e��2elnx��
G�䣨x��= 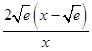 ��
��
��x= ![]() ʱ��G�䣨x��=0����0��x��
ʱ��G�䣨x��=0����0��x�� ![]() ʱ��G�䣨x����0����x��
ʱ��G�䣨x����0����x�� ![]() ʱ��G�䣨x����0��
ʱ��G�䣨x����0��
��x= ![]() ʱ��G��x��ȡ����Сֵ����Сֵ��0��Ҳ����Сֵ��
ʱ��G��x��ȡ����Сֵ����Сֵ��0��Ҳ����Сֵ��
����G��x��=2 ![]() x��e��g��x����0����g��x����2
x��e��g��x����0����g��x����2 ![]() x��e��x��0ʱ�������
x��e��x��0ʱ�������
�ຯ��f��x����g��x������Ψһ�ĸ���ֱ��y=2 ![]() x��e���ʢ���ȷ��
x��e���ʢ���ȷ��
���Դ��ǣ��٢ڢܣ�
�����㾫����������Ҫ�������������ٶ���Ӧ�õ����֪ʶ�㣬��Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ������ȷ�����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
![]() ��
��![]() ������
������![]() �ĵ������䣻
�ĵ������䣻
![]() ������
������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������ߵ���б��Ϊ
�������ߵ���б��Ϊ![]() �����������
�����������![]() ������
������![]() ������
������![]() ���ܲ��ǵ�����������m��ȡֵ��Χ��
���ܲ��ǵ�����������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}�Ǹ����Ϊ�����ĵȲ����У�����a1=1����a2��a4��a6+2�ɵȱ����У�����{bn}��ǰn���ΪSn �� ����2Sn+bn=1
��1��������{an}��{bn}��ͨ�ʽ��
��2�����cn=anbn �� ������{cn}��ǰn���ΪTn �� ��֤��Tn��Sn+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��U=R��A={y|y=2x+1}��B={x|lnx��0}����UA����B=�� ��
A.?
B.{x| ![]() ��x��1}
��x��1}
C.{x|x��1}
D.{x|0��x��1}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=sin��2014x+ ![]() ��+cos��2014x��
��+cos��2014x�� ![]() �������ֵΪA��������ʵ��x1 �� x2 �� ʹ�ö�����ʵ��x����f��x1����f��x����f��x2����������A|x1��x2|����СֵΪ�� ��
�������ֵΪA��������ʵ��x1 �� x2 �� ʹ�ö�����ʵ��x����f��x1����f��x����f��x2����������A|x1��x2|����СֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�ֱ��PA��ƽ��ABCD��AD��BC��AB��AD��BC=2AB=2AD=4BE=4��
��I����֤��ֱ��DE��ƽ��PAC��
������ֱ��PE��ƽ��PAC���ɵĽǵ�����ֵΪ ![]() ��������A��PC��D��ƽ��ǵ�����ֵ��
��������A��PC��D��ƽ��ǵ�����ֵ��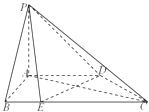
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx+ ![]()
��1����������������ֵ�㣬��ʵ��a��ȡֵ��Χ��
��2�������е�a�� ![]() ��m�ʣ�0��1����n�ʣ�1��+�ޣ�����f��n����f��m������Сֵ��
��m�ʣ�0��1����n�ʣ�1��+�ޣ�����f��n����f��m������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1��������![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f(x)��ax2��bx��c��ͼ����x����������ͬ�Ľ��㣬��f(c)��0��0<x<cʱ��f(x)>0��
(1)֤����![]() ��f(x)��0��һ������
��f(x)��0��һ������
(2)�ԱȽ�![]() ��c�Ĵ�С��
��c�Ĵ�С��
(3)֤������2<b<��1.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com