
(本小题满分12分)
如图,四棱锥 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.
求证:

若 问
问 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求此时平面
的体积最大?并求此时平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
(1)详见解析,(2)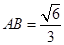 时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
解析试题分析:(1)先将面面垂直转化为线面垂直:ABCD为矩形,故AB AD,又平面PAD
AD,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD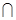 平面ABCD=AD,所以AB
平面ABCD=AD,所以AB 平面PAD,再根据线面垂直证线线垂直:因为PD
平面PAD,再根据线面垂直证线线垂直:因为PD 平面PAD,所以AB
平面PAD,所以AB PD
PD
(2)求四棱锥体积,关键要作出高.这可利用面面垂直性质定理:过P作AD的垂线,垂足为O,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD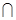 平面ABCD=AD,所以PO
平面ABCD=AD,所以PO 平面ABCD,下面用
平面ABCD,下面用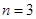 表示高及底面积:设
表示高及底面积:设 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为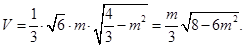 故当
故当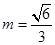 时,即
时,即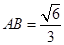 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.
求二面角的余弦值,可利用空间向量求解,根据题意可建立空间坐标系,分别求出平面BPC的法向量及
平面DPC的法向量,再利用向量数量积求夹角余弦值即可.
试题解析:(1)证明:ABCD为矩形,故AB AD,
AD,
又平面PAD 平面ABCD
平面ABCD
平面PAD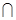 平面ABCD=AD
平面ABCD=AD
所以AB 平面PAD,因为PD
平面PAD,因为PD 平面PAD,故AB
平面PAD,故AB PD
PD
(2)解:过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.
故PO 平面ABCD,BC
平面ABCD,BC 平面POG,BC
平面POG,BC PG
PG
在直角三角形BPC中,
设 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为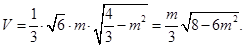
因为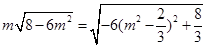
故当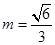 时,即
时,即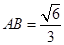 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.
建立如图所示的空间直角坐标系,
故
设平面BPC的法向量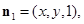 ,则由
,则由 ,
, 得
得
解得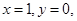
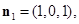
同理可求出平面DPC的法向量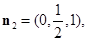 ,从而平面BPC与平面DPC夹角
,从而平面BPC与平面DPC夹角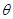 的余弦值为
的余弦值为
考点:面面垂直性质定理,四棱锥体积,利用空间向量求二面角


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB 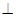 AC, AB=AC=2,
AC, AB=AC=2,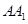 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线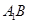 与
与 所成角的余弦值;
所成角的余弦值;
(2)求平面 与
与 所成二面角的正弦值.
所成二面角的正弦值.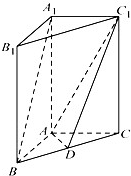
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90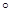 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2.
(1)证明:AC1⊥A1B;
(2)设直线AA1与平面BCC1B1的距离为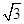 ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,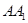 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆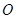 的直径,
的直径,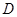 ,
,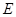 分别是
分别是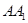 ,
,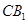 的中点,
的中点,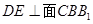 .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥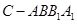 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.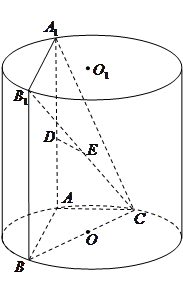
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com