
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
【答案】(1)每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元;(2)商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大;(3)即商店购进70台A型电脑和30台B型电脑才能获得最大利润.
【解析】试题分析:(1)依据题设条件每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元建立方程组![]() 进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
解:(1)设每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元,
则有![]() 解得
解得![]()
即每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元.
(2)①根据题意得y=100x+150(100-x),即y=-50x+15000
②根据题意得100-x≤2x,解得x≥33![]() ,
,
∵y=-50x+15000,-50<0,∴y随x的增大而减小.
∵x为正整数,∴当x=34最小时,y取最大值,此时100-x=66.
即商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大
(3)根据题意得y=(100+m)x+150(100-x),即y=(m-50)x+15000.
33![]() ≤x≤70.
≤x≤70.
①当0<m<50时,m-50<0,y随x的增大而减小.
∴当x =34时,y取得最大值.
即商店购进34台A型电脑和66台B型电脑才能获得最大利润;
②当m=50时,m-50=0,y=15000.
即商店购进A型电脑数最满足33![]() ≤x≤70的整数时,均获得最大利润;
≤x≤70的整数时,均获得最大利润;
③当50<m<100时,m-50>0,y随x的增大而增大.
∴x=70时,y取得最大值.
即商店购进70台A型电脑和30台B型电脑才能获得最大利润.


科目:高中数学 来源: 题型:
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有2个红球,4个白球,除颜色外,它们的形状、大小、质量等完全相同
(1)采用不放回抽样,先后取两次,每次随机取一个球,求恰好取到1个红球,七个白球的概率;
(2)采用放回抽样,每次随机抽取一球,连续取3次,求至少有1次取到红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象上点
图象上点![]() 处的切线方程与直线
处的切线方程与直线![]() 平行(其中
平行(其中![]() ),
),![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() (
(![]() )上的最小值;
)上的最小值;
(Ⅲ)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 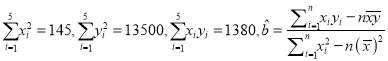 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①函数y=![]() 的定义域为{x|x≥1};
的定义域为{x|x≥1};
②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数对![]() 一切实数
一切实数![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,又
,又![]() .
.
(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在![]() 上的单调性;
上的单调性;
(3)求![]() 在区间
在区间![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com