
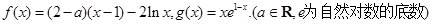
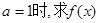 的单调区间;
的单调区间;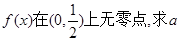 的最小值;
的最小值; ,使得
,使得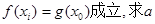 的取值范围。
的取值范围。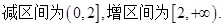 (II)
(II)
 使
使 成立。
成立。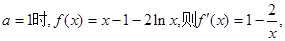 …………1分
…………1分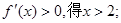 由
由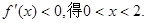
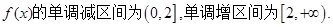 …………3分
…………3分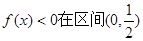 上恒成立不可能,
上恒成立不可能, 上无零点,只要对任意的
上无零点,只要对任意的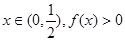 恒成立,
恒成立, 恒成立。 …………4分
恒成立。 …………4分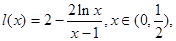
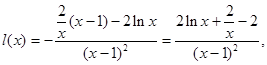 …………5分
…………5分
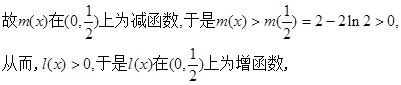
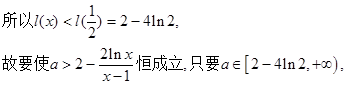

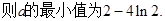 …………6分
…………6分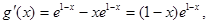
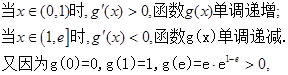
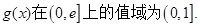 …………7分
…………7分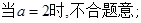
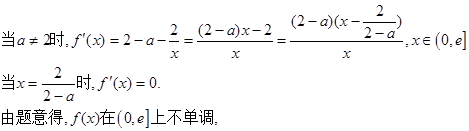
 ① …………9分
① …………9分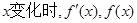 的变化情况如下:
的变化情况如下:| | 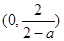 | 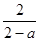 | 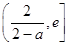 |
 | — | 0 | + |
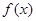 | | 最小值 | |

|
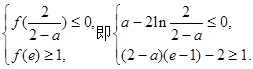
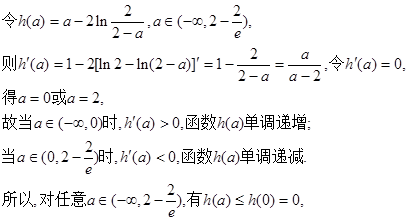
 恒成立。 …………10分
恒成立。 …………10分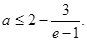 ④
④ 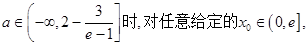
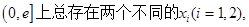
 成立
成立

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com