
若sin α+cos α=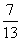 (0<α<π),则tan α=( )
(0<α<π),则tan α=( )
A.-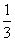 B.
B.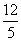 C.-
C.-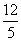 D.
D.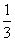
科目:高中数学 来源: 题型:
如图,点P在边长的1的正方形的边上运动,设M是CD边的中点,
 当P沿A→B→C→M运动时,以点P经过的路程
当P沿A→B→C→M运动时,以点P经过的路程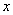 为自变量,
为自变量,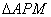
的面积为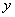 ,则函数
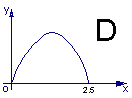
,则函数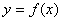 的图象大致是 ( )
的图象大致是 ( )
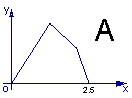
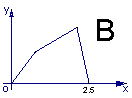
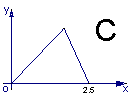
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(sin x,2cos x),b=(2sin x,sin x),设函数f(x)=a·b.
(1)求f(x)的单调递增区间;
(2)若将f(x)的图象向左平移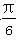 个单位,得到函数g(x)的图象,求函数g(x)在区间
个单位,得到函数g(x)的图象,求函数g(x)在区间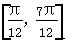 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
A.a2 014=-1,S2 014=2 B.a2 014=-3,S2 014=5
C.a2 014=-3,S2 014=2 D.a2 014=-1,S2 014=5
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.

(1)若直线l的斜率为1,求|AB|的值;
(2)求△PAB的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com