
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
A.a2 014=-1,S2 014=2 B.a2 014=-3,S2 014=5
C.a2 014=-3,S2 014=2 D.a2 014=-1,S2 014=5
科目:高中数学 来源: 题型:
已知向量a=(sin x,-1),b=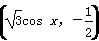 ,函数f(x)=(a+b)·a-2.
,函数f(x)=(a+b)·a-2.
(1)求函数f(x)的最小正周期T;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角,a=2 ,c=4,且f(A)=1,求△ABC的面积S.
,c=4,且f(A)=1,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}是等差数列,a1=tan 225°,a5=13a1,设Sn为数列{(-1)nan}的前n项和,则S2 014=( )
A.2 014 B.-2 014
C.3 021 D.-3 021
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=8x+sin πx-cos πx,数列{an}是公差不为0的等差数列,f(a1)+f(a2)+…+f(a7)=14,则a4=( )
A.0 B.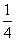 C.
C.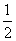 D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=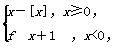 其中[x]表示不超过x的最大整数,如[-1.1]=-2,[π]=3.若直线y=kx+k(k>0)与函数f(x)的图象恰好有3个不同的交点,则实数k的取值范围是( )
其中[x]表示不超过x的最大整数,如[-1.1]=-2,[π]=3.若直线y=kx+k(k>0)与函数f(x)的图象恰好有3个不同的交点,则实数k的取值范围是( )
B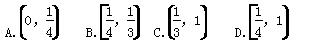
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com