练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量a＝(sin x，－1)，b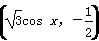＝，函数f(x)＝(a＋b)·a－2.

    (1)求函数f(x)的最小正周期T；

    (2)已知a，b，c分别为△ABC内角A，B，C的对边，其中A为锐角，a＝2，c＝4，且f(A)＝1，求△ABC的面积S.


    解：(1)f(x)＝(a＋b)·a－2

    ＝|a|2＋a·b－2

    ＝sin2x＋1＋sin xcos x＋－2

    ＝＋sin 2x－

    ＝sin 2x－cos 2x

    又a2＝b2＋c2－2bccos A，

    所以12＝b2＋16－2×4b×，

    即b2－4b＋4＝0，则b＝2.

    从而S＝bcsin A＝×2×4×sin＝2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


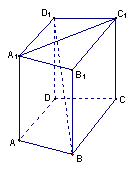
    如图, 在直四棱柱A1B1C1D1-ABCD中，当底面四边形ABCD满足条件__________时, 有A1C1^BD1.(注：填上一种你认为正确的一种条件即可, 不必考虑所有可能的情形.)                                       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝asin 2x＋bcos 2x，其中a，b∈R，ab≠0.若f(x)≤对一切x∈R恒成立，且f>0，则f(x)的单调递增区间是(　　)

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若sin θ，cos θ是方程4x2＋2mx＋m＝0的两个根，则m的值为(　　)

    A．1＋                               B．1－ 

    C．1±                               D．－1－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若α∈的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}的前n项和为Sn，若S2n＝4(a1＋a3＋…＋a2n－1)，a1a2a3＝27，则a6＝(　　)

    A．27                                   B．81 

    C．243                                  D．729

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足an＋1＝an－an－1(n≥2)，a1＝1，a2＝3，记Sn＝a1＋a2＋…＋an，则下列结论正确的是(　　)

    A．a2 014＝－1，S2 014＝2                   B．a2 014＝－3，S2 014＝5

    C．a2 014＝－3，S2 014＝2                   D．a2 014＝－1，S2 014＝5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}的前n项和为Sn，前n项积为∏n，且∏n＝()n(n＋1)，则S5等于(　　)

    A．31                                   B．62 

    C．124                                  D．126

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，设角A，B，C的对边分别为a，b，c。已知B=45°，C=120°，b=2，则c=                （　　）

    A.1     B.   C.2     D.

    查看答案和解析>>

    同步练习册答案