
【题目】在三棱柱![]() 中,已知
中,已知![]() ,点
,点![]() 在底面
在底面![]() 的投影是线段
的投影是线段![]() 的中点
的中点![]() .
.

(1)证明:在侧棱![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 的长;
的长;
(2)求:平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 轴,
轴,![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,该椭圆的离心率为
,该椭圆的离心率为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆交于两个不同的点
与椭圆交于两个不同的点![]() ,求线段
,求线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上截距的取值范围.
轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获![]() (单位:
(单位:![]() )与它的“相近”作物株数
)与它的“相近”作物株数![]() 之间的关系如下表所示:
之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
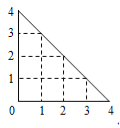
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() ,点
,点![]() .
.
(1)设![]() 是椭圆
是椭圆![]() 上任意的一点,
上任意的一点,![]() 是点
是点![]() 关于坐标原点的对称点,记
关于坐标原点的对称点,记![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)已知点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上在第一象限内的点,记
上在第一象限内的点,记![]() 为经过原点与点
为经过原点与点![]() 的直线,
的直线,![]() 为
为![]() 截直线
截直线![]() 所得的线段长,试将
所得的线段长,试将![]() 表示成直线
表示成直线![]() 的斜率
的斜率![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几何证明选讲
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为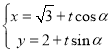 (
(![]() 是参数),以原点
是参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(2)若曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为原点,A,B,C为平面内的三点.求证:
(1) 若A,B,C三点共线,则存在实数α,β,且α+β=1,![]()
(2) 若存在实数α,β,且α+β=1,使得![]() ,则A,B,C三点共线.
,则A,B,C三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com