
【题目】已知![]() 是椭圆
是椭圆![]() 的右焦点,过点
的右焦点,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点.
两点. ![]() 是
是![]() 的中点,直线
的中点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(Ⅰ)求征:![]() ;
;
(Ⅱ)求四边形![]() 面积的最小值.
面积的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,过F且与x轴垂直的直线交该抛物线于A,B两点,|AB|=4.
(1)求抛物线的方程;
(2)过点F的直线l交抛物线于P,Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),其右焦点为F(1,0),离心率为
1(a>b>0),其右焦点为F(1,0),离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F作倾斜角为α的直线l,与椭圆C交于P,Q两点.
(ⅰ)当![]() 时,求△OPQ(O为坐标原点)的面积;
时,求△OPQ(O为坐标原点)的面积;
(ⅱ)随着α的变化,试猜想|PQ|的取值范围,并证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆或双曲线的标准方程:
(1)椭圆的焦点在![]() 轴上,焦距为4,且经过点
轴上,焦距为4,且经过点![]() ;
;
(2)双曲线的焦点在![]() 轴上,右焦点为
轴上,右焦点为![]() ,过
,过![]() 作重直于
作重直于![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,且
两点,且![]() ,离心率为
,离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,过左焦点的直线
,过左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点(异于
两点(异于![]() 、
、![]() 两点),当直线
两点),当直线![]() 垂直于
垂直于![]() 轴时,四边形
轴时,四边形![]() 的面积为6.
的面积为6.
(1)求椭圆的方程;
(2)设直线![]() 、
、![]() 的交点为
的交点为![]() ;试问
;试问![]() 的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
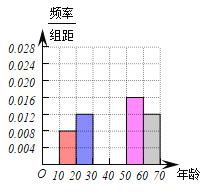
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
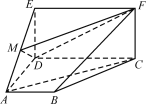
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面MDF将几何体ADE-BCF分成的两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月20日,重庆市实施高考改革方案,2018年秋季入学的高中一年级的学生将实行“![]() ”模式.即“3”为全国统考科目语文、数学、外语所有学生必考;“1”为物理、历史科目中选择一科俗称“2选1”;“2”为再选学科,考生可在化学、生物、思想政治、地理4个科目中选择两科俗称“4选2”,选择学科完全相同即为相同“组合”.某校高一年级有三名同学甲,乙,丙根据自己喜欢的大学和专业情况均选择了物理,为了了解“4选2”选科情况老师找这三名同学来谈话情况如下:
”模式.即“3”为全国统考科目语文、数学、外语所有学生必考;“1”为物理、历史科目中选择一科俗称“2选1”;“2”为再选学科,考生可在化学、生物、思想政治、地理4个科目中选择两科俗称“4选2”,选择学科完全相同即为相同“组合”.某校高一年级有三名同学甲,乙,丙根据自己喜欢的大学和专业情况均选择了物理,为了了解“4选2”选科情况老师找这三名同学来谈话情况如下:
甲说:我选了化学,但没有选思想政治;
乙说:我与甲有一科相同,但没有选化学和地理;
丙说:我与甲有相同的选科,与乙也有相同选科,但我们三个选的“组合”都不相同.则下列结论正确的是( )
A.甲选了化学和地理B.丙可能选化学和思想政治
C.甲一定选地理D.丙一定选了生物和地理
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的一动点,点
上的一动点,点![]() 在直线
在直线![]() 上线段
上线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() .
.
(1)若点![]() 的轨迹为椭圆,则求
的轨迹为椭圆,则求![]() 的取值范围;
的取值范围;
(2)设![]() 时对应的椭圆为
时对应的椭圆为![]() ,
,![]() 为椭圆的右顶点,直线
为椭圆的右顶点,直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com