
【题目】已知椭圆C:![]() 1(a>b>0),其右焦点为F(1,0),离心率为
1(a>b>0),其右焦点为F(1,0),离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点F作倾斜角为α的直线l,与椭圆C交于P,Q两点.
(ⅰ)当![]() 时,求△OPQ(O为坐标原点)的面积;
时,求△OPQ(O为坐标原点)的面积;
(ⅱ)随着α的变化,试猜想|PQ|的取值范围,并证明你的猜想.
【答案】(Ⅰ)![]() 1;(Ⅱ)(i)
1;(Ⅱ)(i)![]() ,(ii)[3,4),证明见解析.
,(ii)[3,4),证明见解析.
【解析】
(Ⅰ)根据题意可得c=1,由离心率![]() ,以及b2=a2﹣c2即可求解.
,以及b2=a2﹣c2即可求解.
(Ⅱ)(i)利用点斜式求出直线l的方程为x![]() y+1,将直线l的方程与椭圆联立,根据韦达定理求出y1+y2,y1y2,进而求出
y+1,将直线l的方程与椭圆联立,根据韦达定理求出y1+y2,y1y2,进而求出![]() ,利用三角形的面积公式即可求解;(ii)设直线l的方程为x=my+1,设P(x1,y1),Q(x2,y2),联立方程组
,利用三角形的面积公式即可求解;(ii)设直线l的方程为x=my+1,设P(x1,y1),Q(x2,y2),联立方程组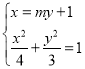 ,利用韦达定理以及弦长公式可求出
,利用韦达定理以及弦长公式可求出![]() ,设m2+1=t,t>1,再利用基本不等式即可求解.
,设m2+1=t,t>1,再利用基本不等式即可求解.
(Ⅰ)由题意可的c=1,
又![]() ,则a=2,
,则a=2,
则b2=a2﹣c2=3,
∴椭圆方程为![]() 1,
1,
(Ⅱ)(i)设直线l的方程为x![]() y+1,设P(x1,y1),Q(x2,y2),
y+1,设P(x1,y1),Q(x2,y2),
联立方程组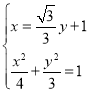 ,消x可得5y2+2
,消x可得5y2+2![]() y﹣9=0,
y﹣9=0,
∴y1+y2![]() ,y1y2
,y1y2![]() ,
,
则|y1﹣y2|![]()
∴S△OPQ![]() |OF||y1﹣y2|
|OF||y1﹣y2|![]() 1
1![]() ,
,
(ii)当α![]() 时,设直线l的方程为x=my+1,则tanα
时,设直线l的方程为x=my+1,则tanα![]() ,
,
设P(x1,y1),Q(x2,y2),
联立方程组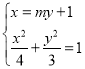 ,消x可得(3m2+4)y2+6my﹣9=0
,消x可得(3m2+4)y2+6my﹣9=0
∴y1+y2![]() ,y1y2
,y1y2![]() ,
,
∴|PQ|![]()
![]()
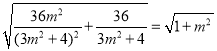
![]() ,
,
设m2+1=t,t>1,
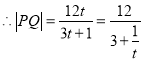 ,∵t>1,∴
,∵t>1,∴![]() ∈(0,1),
∈(0,1),
∴![]() ∈(3,4),∴|PQ|∈(3,4),
∈(3,4),∴|PQ|∈(3,4),
当m=0时,此时α![]() ,此时直线方程为x=1,
,此时直线方程为x=1,
则![]() 1,解得y=±
1,解得y=±![]() ,
,
∴|PQ|=3,
综上所述随着α的变化,|PQ|的取值范围为[3,4).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:
【题目】下列结论正确的是( ).
A.“![]() ,
,![]() 互为共轭复数”是“
互为共轭复数”是“![]() ”的充分不必要条件
”的充分不必要条件
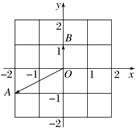
B.如图,在复平面内,若复数![]() ,
,![]() 对应的向量分别是
对应的向量分别是![]() ,
,![]() ,则复数
,则复数![]() 对应的点的坐标为
对应的点的坐标为![]()
C.若函数![]() 恰在
恰在![]() 上单调递减,则实数
上单调递减,则实数![]() 的值为4
的值为4
D.函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 底面
底面![]() ,
,![]() 是
是![]() 上的任意一点.
上的任意一点.
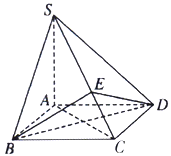
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,是否存在点
,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?如果存在,求出点
?如果存在,求出点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() , 圆
, 圆![]() 在点
在点![]() 处的切线被椭圆
处的切线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于点
于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,O为线段AC的中点,点E在线段A1C1上,则直线OE与平面A1BC1所成角的正弦值的取值范围是( )
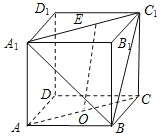
A.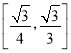 B.
B.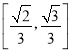 C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,若对任意的n∈N*,数列{an}满足an+1﹣3an<2,则称数列{an}具有性质L.
(Ⅰ)判断下面两个数列是否具有性质L:
①1,3,5,7,9,…;
②1,4,16,64,256,…;
(Ⅱ)若{an}是等差数列且具有性质L,其前n项和Sn满足Sn<2n2+2n(n∈N*),求数列{an}的公差d的取值范围;
(Ⅲ)若{an}是公比为正整数的等比数列且具有性质L,设bn=an![]() (n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
(n∈N*),且数列{bn}不具有性质L,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
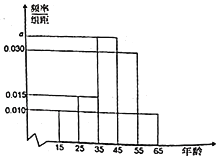
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )

A.BE∥平面PAD,且BE到平面PAD的距离为![]()
B.BE∥平面PAD,且BE到平面PAD的距离为![]()
C.BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D.BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com