
| A. | (-1,$\frac{18}{7}$] | B. | (-1,2] | C. | [2,3) | D. | (-$\frac{6}{7}$,$\frac{18}{7}$] |
分析 该题实质上是二次函数的区间根问题,已知M⊆[1,4],首先分类讨论①M=∅,得出△<0,解出a的范围;②M≠∅,此时△=0或△>0,分三种情况计算a的取值范围,然后综合①②的情况求出实数a的取值范围.
解答 解:设f(x)=x2-2ax+a+2,有△=(-2a)2-4(a+2)=4(a2-a-2),
∵M⊆[1,4]有两种情况:
①M=∅,此时△<0;
当△<0时,-1<a<2,M=∅⊆[1,4];
②其二是M≠∅,此时△=0或△>0,分三种情况计算a的取值范围
当△=0时,a=-1或2;
当a=-1时M={-1}?[1,4];
当a=2时,m={2}⊆[1,4].
当△>0时,a<-1或a>2.
设方程f(x)=0的两根x1,x2,且x1<x2,
那么M=[x1,x2],M⊆[1,4]
∴1≤x1<x2≤4,
∴f(1)≥0且f(4)≥0,1≤a≤4,且△>0,
即 $\left\{\begin{array}{l}{-a+3≥0}\\{18-7a≥0}\\{1≤a≤4}\\{a<-1或a>2}\end{array}\right.$,解得2<a≤$\frac{18}{7}$,
综上讨论知,当M⊆[1,4]时,a的取值范围是(-1,$\frac{18}{7}$],
故选:A.
点评 此题主要考查一元二次不等式的解法,运用了分类讨论的思想,分类讨论的问题比较多,从而加大了试题的难度.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
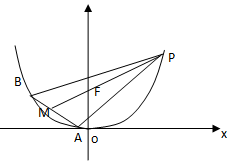 已知△ABP的三个顶点都在抛物线C:x2=4y上,P在第一象限,如图.F为抛物线C的焦点,点M为AB的中点,$\overrightarrow{PF}$=3$\overrightarrow{FM}$,|PF|=3,求直线AB的方程.
已知△ABP的三个顶点都在抛物线C:x2=4y上,P在第一象限,如图.F为抛物线C的焦点,点M为AB的中点,$\overrightarrow{PF}$=3$\overrightarrow{FM}$,|PF|=3,求直线AB的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com