
在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2) < 0的实数x的取值范围为_____________
科目:高中数学 来源: 题型:填空题
三位同学合作学习,对问题“已知不等式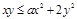 对于
对于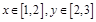 恒成立,求
恒成立,求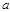 的取值范围”提出了各自的解题思路. 甲说:“可视
的取值范围”提出了各自的解题思路. 甲说:“可视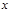 为变量,
为变量,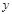 为常量来分析”; 乙说:“不等式两边同除以
为常量来分析”; 乙说:“不等式两边同除以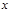 2,再作分析”; 丙说:“把字母
2,再作分析”; 丙说:“把字母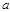 单独放在一边,再作分析”.参考上述思路,或自已的其它解法,可求出实数
单独放在一边,再作分析”.参考上述思路,或自已的其它解法,可求出实数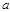 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com