
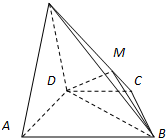
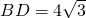 ,AB=2CD=8.
,AB=2CD=8.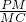 的值;
的值;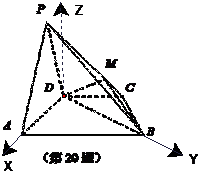 解:(1)连接AC交BD于K,连接MK,则
解:(1)连接AC交BD于K,连接MK,则 ,
,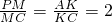 .(6分)
.(6分)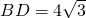 ,AB=8,∴DA⊥DB,
,AB=8,∴DA⊥DB,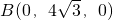 ,
, ,
, ,设点N的坐标为(x0,y0,0),
,设点N的坐标为(x0,y0,0), ,
,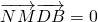 ,
, ,∴
,∴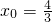 ,
, ,
,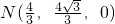 ,(12分)
,(12分)
 ,
, .(14分)
.(14分) ,由PA∥平面MBD,结合直线与平面平行的性质得PA∥MK,利用比例线段即得
,由PA∥平面MBD,结合直线与平面平行的性质得PA∥MK,利用比例线段即得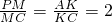 ;
;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com