
【题目】某印刷厂为了研究印刷单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 | 2 | 3 | 4 | 5 | 8 |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
印刷册数 | 2 | 3 | 4 | 5 | 8 | |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
【答案】(1)模型乙的拟合效果更好;(2)印刷8千册对印刷厂更有利.
【解析】试题分析: (1)根据题意,分别计算模型甲和乙的估计值与残差值,填出表格; ②由![]() ,故模型乙的拟合效果更好;(2)设新需求量为
,故模型乙的拟合效果更好;(2)设新需求量为![]() (千册),印刷厂利润为
(千册),印刷厂利润为![]() (元),列出分布列,分别求出期望值比较大小,判断出印刷8千册印刷厂能获得更多利润.
(元),列出分布列,分别求出期望值比较大小,判断出印刷8千册印刷厂能获得更多利润.
试题解析:解:(1)①经计算,可得下表:
印刷册数 | 2 | 3 | 4 | 5 | 8 | |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
残差 | 0.1 | 0 | -0.1 | 0 | 0.1 | |
模型乙 | 估计值 | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
残差 | 0 | 0.1 | 0 | 0 | 0 | |
②![]() ,故模型乙的拟合效果更好;
,故模型乙的拟合效果更好;
(2)若二次印刷8千册,则印刷厂获利为![]() (元),
(元),
若二次印刷10千册,由(1)可知,单册书印刷成本为![]() (元)
(元)
故印刷总成本为16640(元),
设新需求量为![]() (千册),印刷厂利润为
(千册),印刷厂利润为![]() (元),则
(元),则
| 8 | 10 |
| 0.8 | 0.2 |
![]() ,
,
故![]() ,
,
故印刷8千册对印刷厂更有利.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是正四棱柱
是正四棱柱![]() 的一个截面,此截面与棱
的一个截面,此截面与棱![]() 交于点
交于点![]() ,
, ![]() ,其中
,其中![]() 分别为棱
分别为棱![]() 上一点.
上一点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,若四面体
上一点,若四面体![]() 与四棱锥
与四棱锥![]() 的体积相等,求
的体积相等,求![]() 的长.
的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.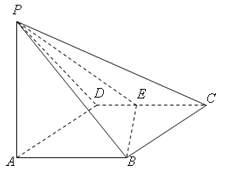
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1= ![]() ,
, 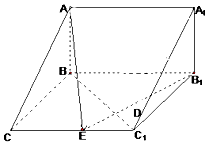
(1)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(2)在(1)的条件下,求AE和BC1所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() (万元).当年产量不小于80千件时,C(x)=51x+
(万元).当年产量不小于80千件时,C(x)=51x+![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
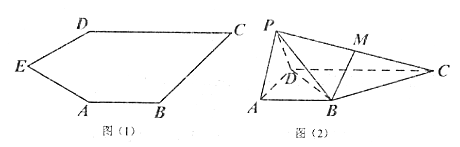
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x , 则有( )
A.f(3)<g(0)<f(4)
B.g(0)<f(4)<f(3)
C.g(0)<f(3)<f(4)
D.f(3)<f(4)<g(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com