
【题目】若函数f(x)=lg(ax﹣1)﹣lg(x﹣1)在区间[2,+∞)上是增函数,则a的取值范围是 .
【答案】![]() <a<1
<a<1
【解析】解:有题意可得:f(x)=lg ![]() ,
,
∵y=lgx在定义域上是单调增函数,且函数f(x)=lg(ax﹣1)﹣lg(x﹣1)在区间[2,+∞)上是增函数,
∴y= ![]() 在[2,+∞)上是增函数,
在[2,+∞)上是增函数,
∴a﹣1<0,∴a<1,
当0<a<1时,函数的定义域为( ![]() ),
),
∴ ![]() ,∴a>
,∴a> ![]() ,
,
当a≤0时,定义域为,
∴ ![]() <a<1,
<a<1,
【考点精析】本题主要考查了函数单调性的性质和对数函数的单调区间的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.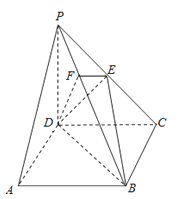
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)求曲线![]() 与
与![]() 焦点的极坐标
焦点的极坐标![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0, ![]() ),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( )
),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 则( ) 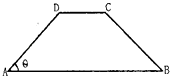
A.随着角度θ的增大,e1增大,e1e2为定值
B.随着角度θ的增大,e1减小,e1e2为定值
C.随着角度θ的增大,e1增大,e1e2也增大
D.随着角度θ的增大,e1减小,e1e2也减小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究印刷单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 | 2 | 3 | 4 | 5 | 8 |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到0.1);
印刷册数 | 2 | 3 | 4 | 5 | 8 | |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为8千册(概率0.8)或10千册(概率0.2),若印刷厂以每册5元的价格将书籍出售给订货商,问印刷厂二次印刷8千册还是10千册能获得更多利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=9内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程; (写一般式)
(2)当直线l的倾斜角为45°时,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为
,设F1、F2分别为椭圆的左、右焦点,椭圆上任意一个动点M到左焦点F1的距离的最大值 为 ![]() +1 (Ⅰ)求椭圆C的方程;
+1 (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线L的斜率为k,且过左焦点F1 , 与椭圆C相交于P、Q两点,若△PQF2的面积为 ![]() ,试求k的值及直线L的方程.
,试求k的值及直线L的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域内的任意x1 , x2(x1≠x2),有以下结论:
①f(0)=1;
②f(1)=0
③f(x1+x2)=f(x1)f(x2)
④f(x1x2)=f(x1)+f(x2)
⑤f( ![]() )<
)< ![]()
⑥f( ![]() )>
)> ![]()
当f(x)=2x时,则上述结论中成立的是(填入你认为正确的所有结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是奇函数,且定义域为(﹣∞,0)∪(0,+∞).若x<0时,f(x)=﹣x﹣1.
(1)求f(x)的解析式;
(2)解关于x的不等式f(x)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com