
【题目】已知函数![]() .
.
(1)设![]() ,(其中
,(其中![]() 是
是![]() 的导数),求
的导数),求![]() 的最小值;
的最小值;
(2)设![]() ,若
,若![]() 有零点,求
有零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求导数,得![]() ,对
,对![]() 再求导,由导数单调性得最小值;
再求导,由导数单调性得最小值;
(2)由(1)知![]() ,因此在
,因此在![]() 时,
时,![]() 无零点,在
无零点,在![]() 时把
时把![]() 函数整理为
函数整理为![]() 的函数:
的函数:![]() ,因
,因![]() ,
,![]() ,故
,故![]() 是
是![]() 的减函数,再分类讨论
的减函数,再分类讨论![]() ,
,![]() ,
,
![]() ,令
,令![]() ,利用导数知识说明函数无零点,
,利用导数知识说明函数无零点,![]() 有一个零点,
有一个零点,![]() 时,用零点存在定理说明函数有零点.为此只要证明
时,用零点存在定理说明函数有零点.为此只要证明![]() ,
,![]() 即可.
即可.
解:(1)![]() ,
,![]() ,定义域为
,定义域为![]()
![]() ,
,![]() 时,
时,![]() ,
,![]() 单减;
单减;![]() 时,
时,![]() ,
,![]() 单增
单增
![]() .
.
(2)①故当![]() 时,由(1)知
时,由(1)知![]() ,故
,故![]() 单增,当
单增,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,故
,故![]() ;而
;而![]() ,故
,故![]() 时,
时,![]() ,此时
,此时![]() 无解;
无解;
![]() ,因
,因![]() ,
,![]() ,故
,故![]() 是
是![]() 的减函数
的减函数
②当![]() 时,
时,![]() ,
,
令![]() ,显然
,显然![]()
![]() ,
,![]() ,
,
![]() ,函数
,函数![]() 单调递增
单调递增
又![]() ,故
,故![]() 时,
时,![]() ,
,![]() 单减;
单减;![]() 时,
时,![]() ,
,![]() 单增,故
单增,故![]() ,
,![]() ,此时
,此时![]() 无解;
无解;
③当![]() 时,
时,![]() ,此时
,此时![]() ,即
,即![]() 有零点;
有零点;
④当![]() 时,
时,![]() ,令
,令![]() 有
有![]() ,下证存在
,下证存在![]() 使得
使得![]() ,
,
![]()
![]() ,令
,令![]() ,
,
令![]() ,则
,则![]()
![]() ,而
,而![]() ,只需
,只需![]()
![]()
记![]() ,
,![]() 单增,
单增,![]() ,故
,故![]() 单增
单增
![]() ,故存在
,故存在![]() ,使得
,使得![]() ,由前
,由前![]() ,故
,故![]() 在
在![]() 有解.
有解.
综上所述,当![]() 时,
时,![]() 有零点
有零点


科目:高中数学 来源: 题型:
【题目】函数![]() 上任意一点
上任意一点![]() 处的切线
处的切线![]() ,在其图像上总存在异与点A的点
,在其图像上总存在异与点A的点![]() ,使得在B点处的切线
,使得在B点处的切线![]() 满足
满足![]() ,则称函数具有“自平行性”.下列有关函数
,则称函数具有“自平行性”.下列有关函数![]() 的命题:
的命题:
①函数![]() 具有“自平行性”;②函数
具有“自平行性”;②函数![]() 具有“自平行性”;
具有“自平行性”;
③函数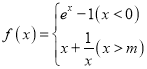 具有“自平行性”的充要条件为实数
具有“自平行性”的充要条件为实数![]() ;
;
④奇函数![]() 不一定具有“自平行性”;⑤偶函数
不一定具有“自平行性”;⑤偶函数![]() 具有“自平行性”.
具有“自平行性”.
其中所有叙述正确的命题的序号是( )
A.①③④B.①④⑤C.②③④D.①②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是我国国家名片之一,高铁的修建凝聚着中国人的智慧与汗水.如图所示,B、E、F为山脚两侧共线的三点,在山顶A处测得这三点的俯角分别为![]() 、
、![]() 、
、![]() ,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
,计划沿直线BF开通穿山隧道,现已测得BC、DE、EF三段线段的长度分别为3、1、2.
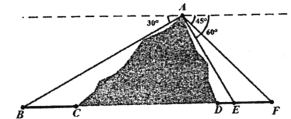
(1)求出线段AE的长度;
(2)求出隧道CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 的距离与它到直线
的距离与它到直线![]() 的距离
的距离![]() 的比值为
的比值为![]() ,设动点
,设动点![]() 形成的轨迹为曲线
形成的轨迹为曲线![]() ..
..
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,过
两点,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为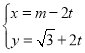 (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为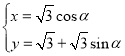 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求曲线
轴正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
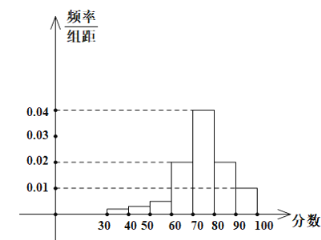
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上所有点横坐标缩短为原来的
上所有点横坐标缩短为原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的取值范围;
的取值范围;
(2)求![]() 中点
中点![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com