
【题目】(本小题满分12分)
已知函数![]() (其中a是实数).
(其中a是实数).
(1)求![]() 的单调区间;
的单调区间;
(2)若设![]() ,且
,且![]() 有两个极值点
有两个极值点![]()
![]() ,求
,求![]() 取值范围.(其中e为自然对数的底数).
取值范围.(其中e为自然对数的底数).
【答案】(1)详见解析(2)![]() ,
,
【解析】试题分析:(1)求出![]() 的定义域
的定义域![]() ,
,![]() ,由此利用导数性质和分类讨论思想能求出
,由此利用导数性质和分类讨论思想能求出![]() 的单调区间.
的单调区间.
(2)推导出![]() ,令
,令![]() ,
,![]() ,则
,则![]() 恒成立,由此能求出
恒成立,由此能求出![]() 的取值范围
的取值范围
试题解析:(1)![]() (其中
(其中![]() 是实数),
是实数),
![]() 的定义域
的定义域![]() ,
,![]() ,
,
令![]() ,
,![]() =
=![]() -16,对称轴
-16,对称轴![]() ,
,![]() ,
,
当![]() =
=![]() -16
-16![]() 0,即-4
0,即-4![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() =
=![]() -16
-16![]() 0,即
0,即![]() 或
或![]()
![]() 若
若![]() ,则
,则![]() 恒成立,
恒成立,
![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间。
,无单调递减区间。
![]() 若
若![]() 4,令
4,令![]() ,得
,得
![]() =
=![]() ,
,![]() =
=![]() ,
,
当![]() (0,
(0,![]() )
)![]() (
(![]() ,+
,+![]() 时,
时,![]() 当
当![]() (
(![]() )时,
)时,![]()
![]() 的单调递增区间为(0,
的单调递增区间为(0,![]() ),(
),(![]() ),单调递减区间为(
),单调递减区间为(![]() )
)
综上所述当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() 时,
时,![]() 的单调递增区间为(0,
的单调递增区间为(0,![]() )和(
)和(![]() ),单调递减区间为(
),单调递减区间为(![]() )
)
(2)由(1)知,若![]() 有两个极值点,则
有两个极值点,则![]() 4,且
4,且![]() ,
,![]() ,
,![]() 又
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,解得
,解得![]() ,
,
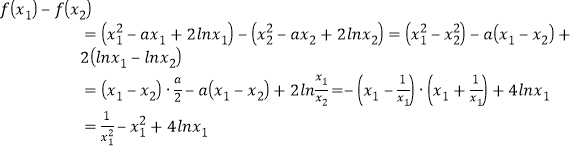
令![]() ,
,![]() 则
则![]() 恒成立
恒成立
![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
即![]()
故![]() 的取值范围为
的取值范围为![]()


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
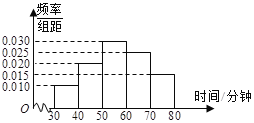
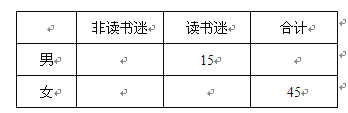
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 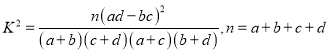
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0 ) 经过点 P(1,
(a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过原点,且在
的图象过原点,且在![]() 处取得极值,直线
处取得极值,直线![]() 与曲线
与曲线![]() 在原点处的切线互相垂直.
在原点处的切线互相垂直.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)若对任意实数的![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是平行四边形ABCD所在平面外一点,E是PD的中点. 
(1)求证:PB∥平面EAC;
(2)若M是CD上异于C、D的点.连结PM交CE于G,连结BM交AC于H,求证:GH∥PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com