
(1)求AD与BG所成角的余弦值;
(2)求二面角B-FB1-E的大小;
(3)求点D到平面B1EF的距离.
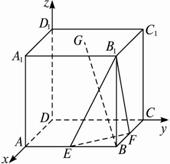
解:建立如图所示的空间直角坐标系D—xyz.?
则A(a,0,0),B(a,a,0),C(0,a,0),E(a,![]() ,0),F(
,0),F(![]() ,a,0),B1(a,a,a),G(
,a,0),B1(a,a,a),G(![]() ,
,![]() ,a).
,a).
 ?
?
(1)∵![]() =(-a,0,0),
=(-a,0,0),![]() =(-
=(-![]() ,-
,-![]() ,a),?
,a),?
∴cos〈![]() ,
,![]() 〉=
〉= =
= =
=![]() .?
.?
∴AD与BG所成角的余弦值为![]() . ?
. ?
(2)设平面B1EF的法向量为n1=(x,y,z).?
∵![]() =(-
=(-![]() ,
,![]() ,0),
,0),![]() =(0,
=(0, ![]() ,a),?
,a),?
∴n1·![]() =0,n1·
=0,n1·![]() =0.?
=0.?
∴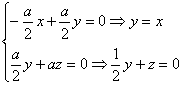
取y=2,则x=2,z=-1.∴可取n1=(2,2,-1).显然DC⊥平面BFB1.?
∴可取平面BFB1的法向量n2=(0,1,0).?
∴cos〈n1,n2〉=![]() =
=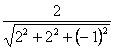 =
=![]() .?
.?
∴所求二面角的大小为arccos![]() . ?
. ?
(3)由(2)已求平面B1EF的法向量n1=(2,2,-1),又![]() =(a,a,a),?
=(a,a,a),?
∴点D到平面B1EF的距离D=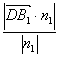 =
=![]() =a.?
=a.?
∴点D到平面B1EF的距离为a.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
在棱长为a的正方体骨架内放置一气球,使其充气且尽可能地膨胀(仍保持球形),则气球表面积的最大值为
[ ]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com