
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)在答题卡上画出这些数据的频率分布直方图(要求用阴影部分显示);
(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
(3)估计这种产品质量指标值的平均值及中位数(其中求平均值时同一组中的数据用该组区间的中点值作代表,求中位数精确到0.1).
【答案】(1)见解析; (2)不能认为该企业生产的这种符合“质量指标值不低于95的产品至少要占全部80%”规定; (3)100;![]() .
.
【解析】
(1)由已知作出频率分布表,由此能作出这些数据的频率分布直方图;
(2)计算质量指标值不低于95的产品所占比例的估计值,由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95的产品至少要占全部产品80%的规定;
(3)由频率分布直方图能求出质量指标值的样本中位数、平均数.
(1)由已知作出频率分布表为:
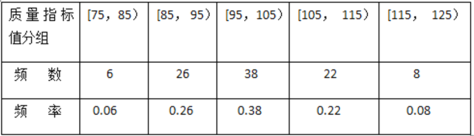
由此绘制频率分布直方图如图:
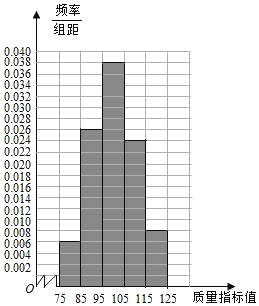
(2)质量指标值不低于95的产品所占比例的估计值为![]() ,
,
由于该估计值小于0.8,故不能认为该企业生产的这种符合“质量指标值不低于95的产品至少要占全部80%”规定;
(3)质量指标值的样本平均数估计值为:
![]() .
.
质量指标值的样本中位数估计值为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).

(1)根据以上数据完成下列![]() 列联表:
列联表:
主食蔬菜 | 主食肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否有99%的把握认为其亲属的饮食习惯与年龄有关?并写出简要分析.
参考公式和数据: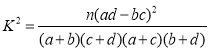 ,
,![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考查某种药物预防疾病的效果,随机抽查了50只服用药的动物和50只未服用药的动得知服用药的动物中患病的比例是![]() ,未服用药的动物中患病的比例为
,未服用药的动物中患病的比例为![]() .
.
(I)根据以上数据完成下列2×2列联表:
患病 | 未患病 | 总计 | |
服用药 | |||
没服用药 | |||
总计 |
(II)能否有99%的把握认为药物有效?并说明理由.
附:
| … | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| … | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数,且
是常数,且![]() )满足条件:
)满足条件:![]() ,且方程
,且方程![]() 有两个相等实根.
有两个相等实根.
(1)求![]() 的解析式;
的解析式;
(2)是否存在实数![]() ,使
,使![]() 的定义域和值域分别为
的定义域和值域分别为![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆上的点到右焦点
,椭圆上的点到右焦点![]() 的距离的最大值为3.
的距离的最大值为3.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作倾斜角不为零的直线
作倾斜角不为零的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,设线段
,设线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com