
如图,四棱锥 中,底面
中,底面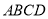 为平行四边形,
为平行四边形,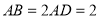 ,
,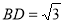 ,
,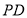 ⊥底面
⊥底面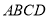 .
.
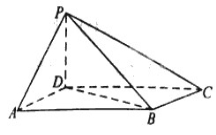
(1)证明:平面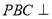 平面
平面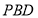 ;
;
(2)若二面角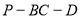 为
为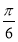 ,求
,求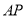 与平面
与平面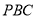 所成角的正弦值.
所成角的正弦值.
(1)证明过程详见解析;(2)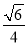 .
.
【解析】
试题分析:(1)可以遵循思路面面垂直 线面垂直
线面垂直 线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明
线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明 面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即
面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即 BD,
BD,  PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
(2)求线面夹角可以利用三维空间直角坐标系,分别以DA,DB,PD三条两两垂直的直线建立坐标系,求面法向量与直线的夹角的余弦值的绝对值即为线面夹角的余弦值.
试题解析:
(1)∵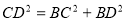 ∴
∴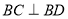
又∵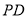 ⊥底面
⊥底面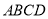 ∴
∴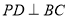
又∵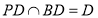 ∴
∴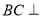 平面
平面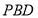
而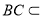 平面
平面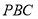 ∴平面
∴平面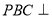 平面
平面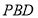 5分
5分
(1)由(1)所证,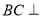 平面
平面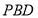 ,所以∠
,所以∠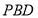 即为二面角P-BC-D的平面角,即∠
即为二面角P-BC-D的平面角,即∠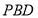
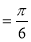
而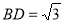 ,所以
,所以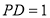 7分
7分
分别以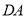 、
、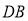 、
、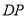 为
为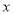 轴、
轴、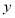 轴、
轴、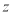 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则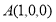 ,
,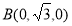 ,
,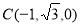 ,
, 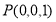 ,所以,
,所以,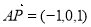 ,
,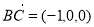 ,
,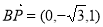 ,设平面
,设平面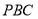 的法向量为
的法向量为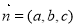 ,则
,则 ,即
,即 可解得
可解得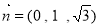 ∴
∴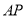 与平面
与平面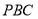 所成角的正弦值为
所成角的正弦值为 12分
12分
考点:面面垂直 线面夹角


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试文科数学试卷(解析版) 题型:解答题
在公差不为0的等差数列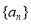 中,
中,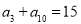 ,且
,且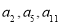 成等比数列.
成等比数列.
(1)求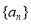 的通项公式;
的通项公式;
(2)设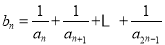 ,试比较
,试比较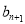 与
与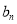 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:解答题
设不等式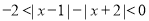 的解集为M,
的解集为M,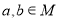 .
.
(1)证明: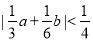 ;
;
(2)比较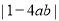 与
与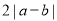 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试文科数学试卷(解析版) 题型:选择题
执行左下面的程序框图,如果输入的依次为3,5,3,5,4,4,3,4,4,则输出的S为( )
A.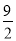 B.4 C.
B.4 C.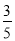 D.
D.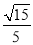
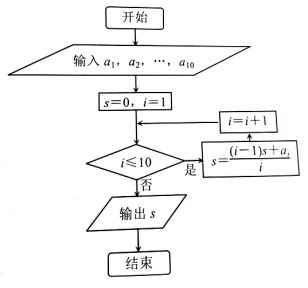
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:解答题
设函数
(1)若 时,解不等式
时,解不等式 ;
;
(2)若不等式 的对一切
的对一切 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:选择题
设m,n分别是先后抛掷一枚骰子得到的点数,则在先后两次出现的点数中有5的条件下,方程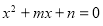 有实根的概率为( )
有实根的概率为( )
A.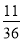 B.
B.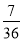 C.
C.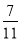 D.
D.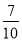
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
已知双曲线 上一点
上一点 ,过双曲线中心的直线交双曲线于
,过双曲线中心的直线交双曲线于 两点,记直线
两点,记直线 的斜率分别为
的斜率分别为 ,当
,当 最小时,双曲线离心率为( )
最小时,双曲线离心率为( )
A. B.
B. C
C D
D
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三年级模拟考试文科数学试卷(解析版) 题型:解答题
如右图,在底面为平行四边形的四棱柱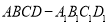 中,
中,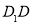
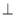 底面
底面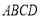 ,
,
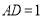 ,
,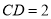 ,
, .
.
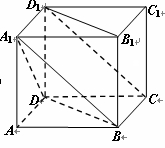
(1)求证:平面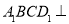 平面
平面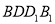 ;
;
(2)若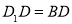 ,求四棱锥
,求四棱锥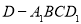 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com