
(本题13分)最近北方遭受雪灾,蔬菜告急,南方某蔬菜公司要将一批蔬菜从南方A地运到北方B地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 | 途中速度 (km/h) | 途中费用 (元/km) | 装卸时间 (h) | 装卸费用 (元) |
| 汽车 | 50 | 8 | 2 | 1000 |
| 火车 | 100 | 4 | 4 | 2000 |
若这批蔬菜在运输过程(含装卸时间)中损耗为300元/h,设A、B 两地距离为![]() km
km
(I)设采用汽车与火车运输的总费用分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的表达式;
的表达式;
(II)试根据A、B两地距离大小比较采用哪种运输工具比较好(即运输总费用最小).
(注:总费用=途中费用+装卸费用+损耗费用)
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源:2011届福建省福州市八县(市)协作校高三上学期期中联考理科数学卷 题型:解答题
(本题13分)
已知集合A={x|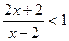 },B={x|x2>5-4x},C={x│|x-m|<1,m∈R}。
},B={x|x2>5-4x},C={x│|x-m|<1,m∈R}。
(1)求A∩B;
(2)若(A∩B)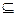 C,求m的取值范围。
C,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014届浙江舟山二中等三校高二上学期期末联考理科数学试卷(解析版) 题型:解答题
(本题13分)设椭圆 的左右焦点分别为
的左右焦点分别为 ,
, ,上顶点为
,上顶点为 ,过点
,过点 与
与 垂直的直线交
垂直的直线交 轴负半轴于
轴负半轴于 点,且
点,且 是
是 的中点.
的中点.

(1)求椭圆的离心率;
(2)若过点 的圆恰好与直线
的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题13分)已知函数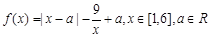 。
。
(Ⅰ)若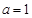 ,试判断并证明
,试判断并证明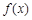 的单调性;
的单调性;
(Ⅱ)若函数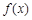 在
在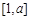 上单调,且存在
上单调,且存在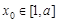 使
使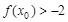 成立,求
成立,求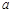 的取值范围;
的取值范围;
(Ⅲ)当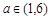 时,求函数
时,求函数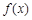 的最大值的表达式
的最大值的表达式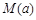 。
。
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二上学期期中考试数学理卷 题型:解答题
(本题13分) 已知点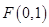 ,直线
,直线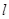 :
: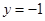 ,
,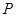 为平面上的动点,过点
为平面上的动点,过点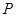 作直线
作直线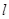 的垂线,垂足为
的垂线,垂足为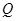 ,且
,且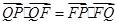 .
.
(1)求动点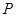 的轨迹
的轨迹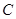 的方程;
的方程;
(2)已知圆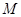 过定点
过定点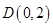 ,圆心
,圆心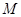 在轨迹
在轨迹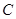 上运动,且圆
上运动,且圆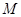 与
与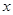 轴交于
轴交于 、
、 两点,设
两点,设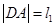 ,
,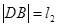 ,求
,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com