
(本题13分)已知函数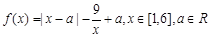 。
。
(Ⅰ)若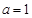 ,试判断并证明
,试判断并证明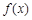 的单调性;
的单调性;
(Ⅱ)若函数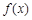 在
在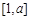 上单调,且存在
上单调,且存在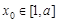 使
使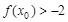 成立,求
成立,求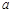 的取值范围;
的取值范围;
(Ⅲ)当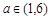 时,求函数
时,求函数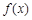 的最大值的表达式
的最大值的表达式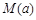 。
。
(Ⅰ)用定义证明函数的单调性;(Ⅱ)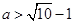 ;(Ⅲ)
;(Ⅲ)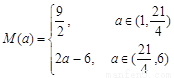 。
。
【解析】
试题分析:(Ⅰ)当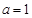 时,
时,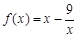 在
在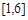 上单调递增
1分
上单调递增
1分
证明: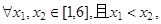 1分
1分
则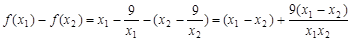
 2分
2分
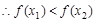 ,
,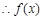 在
在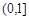 上单调递增。
上单调递增。
(Ⅱ)当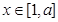 时,
时,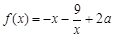
由于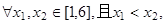
则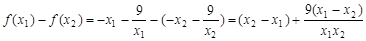
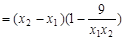
则当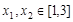 时,
时,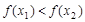 ,
,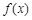 单调增;
单调增;
当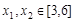 时,
时,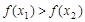 ,
,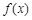 单调减。
单调减。
所以,当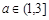 时,
时,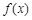 在
在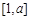 上单调增;
2分
上单调增;
2分
又存在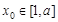 使
使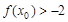 成立
成立
所以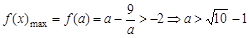 。
2分
。
2分
综上,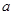 的取值范围为
的取值范围为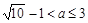 。
。
(Ⅲ)当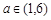 时,
时,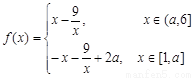
由(Ⅰ)知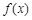 在区间
在区间 上单调递增, 1分
上单调递增, 1分
由(Ⅱ)知,①当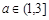 时,
时,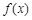 在
在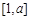 上单调增,
上单调增,
②当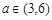 时,
时,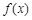 在
在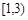 上单调递增,在
上单调递增,在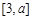 上单调递减,
上单调递减,
又因为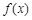 在
在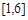 上是连续函数
上是连续函数
所以,①当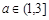 时,
时,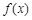 在
在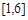 上单调增,则
上单调增,则 ;
;
②当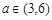 时,
时,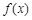 在
在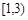 上单调增,在
上单调增,在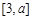 上单调减,在
上单调减,在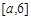 上单调增,
上单调增,
2分
则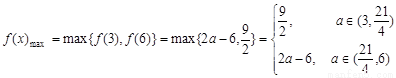
综上,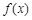 的最大值的表达式
的最大值的表达式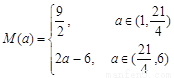 。
2分
。
2分
考点:函数的单调性;函数的最值;基本不等式。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: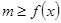 在
在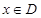 上恒成立
上恒成立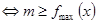 ;思路2:
;思路2: 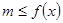 在
在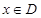 上恒成立
上恒成立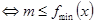 。注意恒成立问题与存在性问题的区别。
。注意恒成立问题与存在性问题的区别。


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
(本题13分)已知函数f (x) = ln(ex + a)(a为常数)是实数集R上的奇函数,函数g (x) =
![]() f (x) + sinx是区间[1,1]上的减函数.
f (x) + sinx是区间[1,1]上的减函数.
(1)求a的值;
(2)若g (x)≤t2 +![]() t + 1在x∈[1,1]上恒成立,求t的取值范围;
t + 1在x∈[1,1]上恒成立,求t的取值范围;
(3)讨论关于x的方程![]() 的根的个数.
的根的个数.
查看答案和解析>>
科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考理数 题型:解答题
(本题13分)
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在
在 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二3月月考文科数学试卷 题型:解答题
(本题13分)
已知函数
 (1)当
(1)当 时,判断函数
时,判断函数 在其定义域内是否存在极值?若存在,求出极值,若不存在,说明理由(2)若函数
在其定义域内是否存在极值?若存在,求出极值,若不存在,说明理由(2)若函数 在其定义域内为单调函数,求
在其定义域内为单调函数,求 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校联考高一第三次月考数学卷 题型:解答题
(本题13分)
已知函数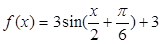 ,
,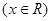

(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由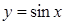 ,
,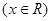 的图象经怎样的变换得到.
的图象经怎样的变换得到.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com