
(本题13分)已知函数f (x) = ln(ex + a)(a为常数)是实数集R上的奇函数,函数g (x) =
![]() f (x) + sinx是区间[1,1]上的减函数.
f (x) + sinx是区间[1,1]上的减函数.
(1)求a的值;
(2)若g (x)≤t2 +![]() t + 1在x∈[1,1]上恒成立,求t的取值范围;
t + 1在x∈[1,1]上恒成立,求t的取值范围;
(3)讨论关于x的方程![]() 的根的个数.
的根的个数.
解析:(1)由于f (x) 是R上的奇函数,f (0) = 0,故a = 0.……………………3分
(2)∵g (x)在[1,1]上单调递减,∴![]() 时
时![]() 恒成立
恒成立
![]() ,
,![]()
∴只要![]()
∴(t + 1)![]() + t2 + sin1 + 1≥0(其中
+ t2 + sin1 + 1≥0(其中![]() ≤1)恒成立.……………………5分
≤1)恒成立.……………………5分
令![]()
则![]()
∴t≤1.………………………………………………………………………………8分
(3)由(1)知![]() .∴方程为
.∴方程为![]()
令f1(x) =![]() ,f2(x) = x2 2ex + m,
,f2(x) = x2 2ex + m,
∵![]()
当x∈(0,e)时,![]() ,∴
,∴![]() 在(0,e]上为增函数;
在(0,e]上为增函数;
当x∈(e,+∞)时,![]() ,∴
,∴![]() 在(e,+∞)上为减函数;
在(e,+∞)上为减函数;
当x = e时![]() .
.
而![]()
∴当![]() 时,即
时,即![]() 时方程无解.
时方程无解.
当![]() 时,即
时,即![]() 时方程有一解.
时方程有一解.
当![]() 时,即
时,即![]() 时方程有二解.………………………………………13分
时方程有二解.………………………………………13分


科目:高中数学 来源:2011届陕西省师大附中、西工大附中高三第七次联考理数 题型:解答题
(本题13分)
已知函数 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在
在 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题13分)已知函数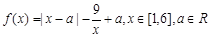 。
。
(Ⅰ)若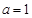 ,试判断并证明
,试判断并证明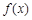 的单调性;
的单调性;
(Ⅱ)若函数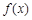 在
在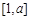 上单调,且存在
上单调,且存在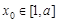 使
使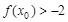 成立,求
成立,求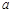 的取值范围;
的取值范围;
(Ⅲ)当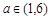 时,求函数
时,求函数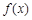 的最大值的表达式
的最大值的表达式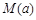 。
。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省无为县四高三考文科数学试卷(解析版) 题型:解答题
(本题满分13分)已知函数f(x)=cos(-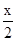 )+cos(
)+cos(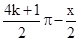 ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)=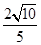 ,α∈(0,
,α∈(0,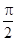 ),求tan(2α+
),求tan(2α+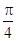 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源:2010年福建省四地六校联考高一第三次月考数学卷 题型:解答题
(本题13分)
已知函数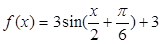 ,
,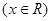

(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由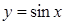 ,
,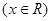 的图象经怎样的变换得到.
的图象经怎样的变换得到.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com