
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
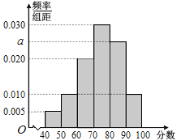
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若向量列![]() ,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即
,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即![]() (
(![]() ,且
,且![]() ,
,![]() 为常向量),则称这个向量列
为常向量),则称这个向量列![]() 为等差向量列,这个常向量叫做等差向量列的公差,且向量列
为等差向量列,这个常向量叫做等差向量列的公差,且向量列![]() 的前
的前![]() 项和为
项和为![]() .已知等差向量列
.已知等差向量列![]() 满足
满足![]() ,则向量列
,则向量列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.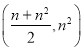 B.
B.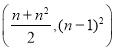
C.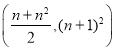 D.
D.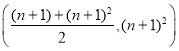
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知衡量病毒传播能力的最重要指标叫做传播指数RO.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是:![]() 确认病例增长率
确认病例增长率![]() 系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为
系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为![]() ,两例连续病例的间隔时间的平均数为
,两例连续病例的间隔时间的平均数为![]() 天,根据以上RO数据计算,若甲得这种传染病,则
天,根据以上RO数据计算,若甲得这种传染病,则![]() 轮传播后由甲引起的得病的总人数约为( )
轮传播后由甲引起的得病的总人数约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
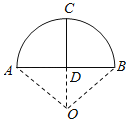
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
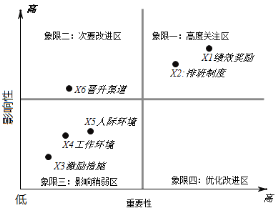
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
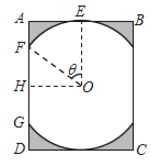
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
,![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1![]() ,且
,且![]() ,设
,设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com