已知数列{an},{bn}满足a1=2,2an=1+anan+1,bn=an-1,设数列{bn}的前n项和为Sn,令Tn=S2n-Sn.
(Ⅰ)求数列{bn}的通项公式; (Ⅱ)判断Tn+1,Tn(n∈N*)的大小,并说明理由.
解:(Ⅰ)解:由b
n=a
n-1得
a
n=b
n+1代入2a
n=1+a
na
n+1得2(b
n+1)=1+(b
n+1)(b
n+1+1)
整理得b
nb
n+1+b
n+1-b
n=0
从而有

∴b
1=a
1-1=2-1=1
∴
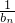
是首项为1,公差为1的等差数列,
∴

(Ⅱ)T
n+1>T
n证明:∵
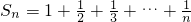
∴T
n=S
2n-S
n=
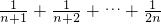
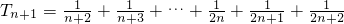

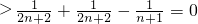
故T
n+1>T
n分析:(I)将两个已知等式结合得到关于数列{b
n}的项的递推关系,构造新数列,利用等差数列的通项公式求出

,进一步求出b
n.
(II)表示出T
n,T
n+1,求出T
n+1-T
n,通过放缩法,判断出此差的符号,判断出T
n+1,T
n两者的大小.
点评:求数列的通项公式时,一般先看递推关系的特点选择合适的求通项的方法;求数列的前n项和一般也是先判断通项的特点,再选择合适的方法.


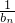 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
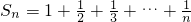
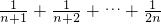
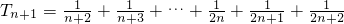

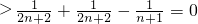
 ,进一步求出bn.
,进一步求出bn.
