

思路分析:根据题意要分清以下两点:其一,台风中心到O点的距离怎样用时间t表示出来;其二,O点受台风侵袭的条件是什么?
解:设t h后该城市受到侵袭,此时台风侵袭的圆形区域半径为(10t+60) km,连结AO,
由余弦定理知OA2=OP2+PA2-2·OP·PA·cos∠OPA,
由于OP=300 km,PA=20t,∠APO=θ-45°,
∴cos∠OPA=cos(θ-45°)=cosθ·cos45°+sinθsin45°=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() ,
,
故OA2=3002+(20t)2-2×300×20t×![]() =202·t2-9 600t+3002≤(10t+60)2,
=202·t2-9 600t+3002≤(10t+60)2,
即t2-36t+288≤0,
解得12≤t≤24.


科目:高中数学 来源: 题型:
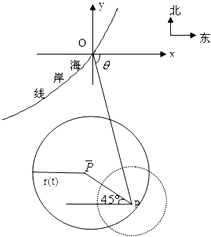 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南θ(cosθ=
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南θ(cosθ=
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 θ(cosθ=
在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南 θ(cosθ=
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2014届江西省高一下学期第一次月考数学(解析版)理科重点班 题型:解答题
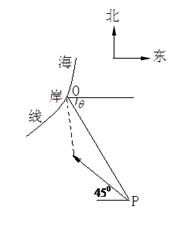
在某海滨城市附近海面上有一台风,据监测,当前台风中心位于城市O的东偏南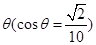 方向300
方向300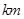 的海面P处,并以
的海面P处,并以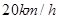 的速度向西偏北
的速度向西偏北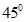 方向移动。台风侵袭的范围为圆形区域,当前半径为60
方向移动。台风侵袭的范围为圆形区域,当前半径为60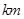 ,并以
,并以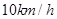 的速度不断增大,问几时后该城市开始受到台风的侵袭?
的速度不断增大,问几时后该城市开始受到台风的侵袭?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com