
| a+b |
| 2 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
| a2+b2 |
| 2 |
| a2-b2 |
| a-b |
1±
| ||
| 2 |
1+
| ||
| 2 |
1-
| ||
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
(
|
5+2
|
(
|
5-2
|
| 1 |
| 2 |
5+2
|
5-2
|
| ||
| 2 |
1-
| ||
| 2 |
3-
| ||
| 2 |
1+
| ||
| 2 |
3+
| ||
| 2 |
| ||
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
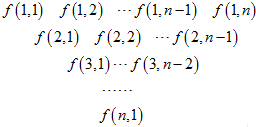 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.| 1 |
| aiai+1 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图.
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图,如图.. |
| X |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在椭圆C:
在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| q |
| p |
| q |
| π |
| 4 |
| a-b |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| f(x) |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com