
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() 交
交![]() 于
于![]() 点,
点,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】现有长分别为![]() 、
、![]() 、
、![]() 的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取
的钢管各3根(每根钢管的质地均匀、粗细相同且富有不同的编号),从中随机抽取![]() 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的,![]() ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(I)当![]() 时,记事件
时,记事件![]() ,求
,求![]() ;
;
(II)当![]() 时,若用
时,若用![]() 表示新焊成的钢管的长度(焊接误差不计),求
表示新焊成的钢管的长度(焊接误差不计),求![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过曲线C:y![]() x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
(1)求证:x1x2=﹣16;
(2)曲线C分别在点A,B处的切线(与C只有一个公共点,且C在其一侧的直线)交于点M,求点M的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学图书馆举行高中志愿者检索图书的比赛,从高一、高二两个年级各抽取10名志愿者参赛。在规定时间内,他们检索到的图书册数的茎叶图如图所示,规定册数不小于20的为优秀.
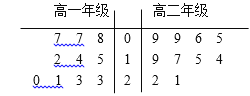
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人,求抽取的4人中至少一人优秀的概率;
(Ⅱ) 从高一10名志愿者中抽取一人,高二10名志愿者中抽取两人,3人中优秀人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com