
分析 (Ⅰ)由题意a=2b,根据椭圆C上任意一点到椭圆左右两个焦点的距离之和为4,利用椭圆的定义求出a,可得b,即可求椭圆C的方程;
(Ⅱ)设直线MN:x=my-1,联立椭圆方程,消去x,运用韦达定理,再由△AMN面积为S=$\frac{1}{2}$|AD|•|y1-y2|,代入化简整理,再由对勾函数的性质,即可得到最大值.
解答 解:(Ⅰ)由题意a=2b,…(2分)
又2a=4,所以a=2,b=1…(4分)
椭圆方程为$\frac{x^2}{4}+{y^2}=1$…(5分)
(Ⅱ)A点坐标为(-2,0),直线MN过定点(-1,0),
∴令直线MN的方程为x=my-1,…(6分)
联立$\left\{{\begin{array}{l}{x=my-1}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$,消去x得(m2+4)y2-2my-3=0,…(8分)
∴${y_1}+{y_2}=\frac{2m}{{{m^2}+4}}$,${y_1}{y_2}=\frac{-3}{{{m^2}+4}}$,…(9分)
${S_{△AMN}}=\frac{1}{2}|{AD}||{{y_1}-{y_2}}|=\frac{1}{2}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$…(11分)
=$\frac{1}{2}\sqrt{\frac{{4{m^2}}}{{{{({m^2}+4)}^2}}}+\frac{12}{{{m^2}+4}}}$=$2\sqrt{\frac{{{m^2}+3}}{{{{({m^2}+4)}^2}}}}$,…(12分)
令t=m2+3,t≥3,
∴${S_{△AMN}}=2\sqrt{\frac{t}{{{{(t+1)}^2}}}}=2\sqrt{\frac{1}{{t+\frac{1}{t}+2}}}≤2\sqrt{\frac{1}{{3+\frac{1}{3}+2}}}=\frac{{\sqrt{3}}}{2}$,…(14分)
当且仅当t=m2+3=3即m=0时,△AMN面积的最大值为$\frac{{\sqrt{3}}}{2}$.…(15分)
点评 本题考查椭圆的方程和性质,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,以及化简整理的运算能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
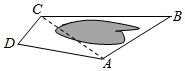 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.
设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=μ$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com