
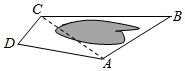
 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
分析 分别在△ACD,ABC中使用余弦定理计算cosB,cosD,令cosB+cosD=0解出AC.
解答 解:在△ACD中,由余弦定理得:cosD=$\frac{A{D}^{2}+C{D}^{2}-A{C}^{2}}{2AD•CD}$=$\frac{34-A{C}^{2}}{30}$,
在△ABC中,由余弦定理得:cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{89-A{C}^{2}}{80}$.
∵B+D=180°,∴cosB+cosD=0,即$\frac{34-A{C}^{2}}{30}$+$\frac{89-A{C}^{2}}{80}$=0,
解得AC=7.
故选:A.
点评 本题考查了余弦定理解三角形,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3]∪[1,+∞) | B. | [-3,1] | C. | [1,+∞) | D. | (-∞,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方 向移动,距风暴中心450km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为( )
如图,据气象部门预报,在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方 向移动,距风暴中心450km以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为( )| A. | 14h | B. | 15h | C. | 16h? | D. | 17h |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{{\sqrt{2}}}{2}$) | B. | ($\frac{{\sqrt{2}}}{2}$,1) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
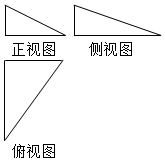 己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )
己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )| A. | $\frac{28\sqrt{14}}{3}$π | B. | $\frac{56\sqrt{14}}{3}$π | C. | $\frac{7\sqrt{14}}{3}$π | D. | $\frac{7\sqrt{14}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com