
 如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.分析 (1)由已知条件推导出△PAB∽△PCA,AD是∠BAC的角平分线,由此能够证明PA•DC=PC•DB.
(2)由切割线定理求出PC=40,BC=30,由已知条件条件推导出△ACE∽△ADB,由此能求出AD•AE的值
解答 证明:(Ⅰ)∵AP为圆O的切线,∴∠PAB=∠ACP,
又∠P为公共角,∴△PAB∽△PCA,
∴$\frac{AB}{AC}$=$\frac{AP}{PC}$,
∵AD是∠BAC的角平分线,∴$\frac{DB}{DC}=\frac{AB}{AC}$.
∴$\frac{DB}{DC}=\frac{AP}{PC}$,∴PA•DC=PC•DB. …(5分)
(2)解:∵PA为圆O的切线,BC是过点O的割线,
∴PA2=PB•PC,
∴PC=9,BC=8,
又∵∠CAB=90°,∴AC2+AB2=BC2=64,
又由(Ⅰ)知$\frac{AB}{AC}$=$\frac{AP}{PC}$=$\frac{3}{9}=\frac{1}{3}$,
∴$AC=\frac{{12\sqrt{10}}}{5},AB=\frac{{4\sqrt{10}}}{5}$,
连接EC,则∠CAE=∠EAB,
∴△ACE∽△ADB,∴$\frac{AB}{AE}$=$\frac{AD}{AC}$,
∴AD•AE=AB•AC=$\frac{4\sqrt{10}}{5}•\frac{12\sqrt{10}}{5}$=$\frac{96}{5}$.…(10分)
点评 本题考查三角形相似的证明和应用,考查线段乘积的求法,是中档题,解题时要注意切割线定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
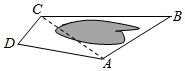 如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.
如图,为了测量A、C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为( )km.| A. | 7 | B. | 8 | C. | 9 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com