
分析 (1)若a=$\frac{1}{2}$,求函数的导数,利用函数单调性和导数之间的关系即可求函数f(x)的单调区间;
(2)根据函数与方程之间的关系转化为函数存在零点问题,构造函数,求函数的导数,利用函数极值和函数零点之间的关系进行转化求解即可.
解答 解:(1)若a=$\frac{1}{2}$,F(x)=(x2+bx+1)ex,
则F′(x)=(2x+b)ex+(x2+bx+1)ex=[x2+(b+2)x+b+1]ex=(x+1)[x+(b+1)]ex,
由F′(x)=0得(x+1)[x+(b+1)]=0,即x=-1或x=-(b+1),
①若b+1=1,即b=0时,F′(x)=(x+1)2ex≥0,此时函数单调递增,单调递增区间为(-∞,+∞),
②若-(b+1)<-1,即b>0时,由F′(x)>0得(x+1)[x+(b+1)]>0,即x>-1或x<-(b+1),
此时函数单调递增,单调递增区间为(-∞,-(b+1)),(-1,+∞),
由F′(x)<0得(x+1)[x+(b+1)]<0,即-(b+1)<x<-1,
此时函数单调递减,单调递减区间为(-(b+1),-1),
③若-(b+1)>-1,即b<0时,由F′(x)>0得(x+1)[x+(b+1)]>0,解得:x>-(b+1)或x<-1,
此时函数单调递增,单调递增区间为(-∞,-1),(-(b+1),+∞),
由F′(x)<0得(x+1)[x+(b+1)]<0,解得:-1<x<-(b+1),
此时函数单调递减,单调递减区间为(-1,-(b+1));
(2)方程f(x)=ex在(0,1)内有解,即2ax2+bx+1=ex在(0,1)内有解,
即ex-2ax2-bx-1=0,
设g(x)=ex-2ax2-bx-1,
则g(x)在(0,1)内有零点,
设x0是g(x)在(0,1)内的一个零点,
则g(0)=0,g(1)=0,知函数g(x)在(0,x0)和(x0,1)上不可能单调递增,也不可能单调递减,
设h(x)=g′(x),
则h(x)在(0,x0)和(x0,1)上存在零点,
即h(x)在(0,1)上至少有两个零点,
g′(x)=ex-4ax-b,h′(x)=ex-4a,
当a≤$\frac{1}{4}$时,h′(x)>0,h(x)在(0,1)上递增,h(x)不可能有两个及以上零点,
当a≥$\frac{e}{4}$时,h′(x)<0,h(x)在(0,1)上递减,h(x)不可能有两个及以上零点,
当$\frac{1}{4}$<a<$\frac{e}{4}$时,令h′(x)=0,得x=ln(4a)∈(0,1),
则h(x)在(0,ln(4a))上递减,在(ln(4a),1)上递增,h(x)在(0,1)上存在最小值h(ln(4a)).
若h(x)有两个零点,则有h(ln(4a))<0,h(0)>0,h(1)>0,
h(ln(4a))=4a-4aln(4a)-b=6a-4aln(4a)+1-e,$\frac{1}{4}$<a<$\frac{e}{4}$,
设φ(x)=$\frac{3}{2}$x-xlnx+1-x,(1<x<e),
则φ′(x)=$\frac{1}{2}$-lnx,
令φ′(x)=$\frac{1}{2}$-lnx=0,得x=$\sqrt{e}$,
当1<x<$\sqrt{e}$时,φ′(x)>0,此时函数φ(x)递增,
当$\sqrt{e}$<x<e时,φ′(x)<0,此时函数φ(x)递减,
则φ(x)max=φ($\sqrt{e}$)=$\sqrt{e}$+1-e<0,
则h(ln(4a))<0恒成立,
由h(0)=1-b=2a-e+2>0,h(1)=e-4a-b>0,
得$\frac{e-2}{2}$<a<$\frac{1}{2}$,
当$\frac{e-2}{2}$<a<$\frac{1}{2}$时,设h(x)的两个零点为x1,x2,则g(x)在(0,x1)递增,
在(x1,x2)上递减,在(x2,1)递增,
则g(x1)>g(0)=0,
g(x2)<g(1)=0,
则g(x)在(x1,x2)内有零点,
综上,实数a的取值范围是($\frac{e-2}{2}$,$\frac{1}{2}$).
点评 本题主要考查函数单调性和单调区间的求解和判断,利用函数单调性的性质以及函数单调性和导数之间的关系是解决本题的关键,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
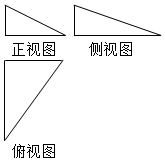 己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )
己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )| A. | $\frac{28\sqrt{14}}{3}$π | B. | $\frac{56\sqrt{14}}{3}$π | C. | $\frac{7\sqrt{14}}{3}$π | D. | $\frac{7\sqrt{14}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B、C两点,PA=3,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{3π}{2}$ | C. | $\frac{\sqrt{3}π}{4}$ | D. | $\frac{\sqrt{3}π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>3} | B. | {x|x<0或x>2} | C. | {x|x<0或x>3} | D. | {x|x<-1或x>3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com