
分析 (Ⅰ)由开口方向和最大值,可得a,b的关系,由区间内单调,可得a,b关系,两者结合得到范围.
(Ⅱ)对对称轴进行分类讨论,由此得到最值的绝对值小于等于1,得到a的范围.
解答 解:(Ⅰ)f($\frac{a}{2b}$)=1,∴$\frac{{a}^{2}}{4b}$=1,∴a=2$\sqrt{b}$,
又$\frac{a}{2b}$≥1,∴2b≤a,
∴2b≤2$\sqrt{b}$,∴b≤1,
(Ⅱ)①当$\frac{a}{b}$>1时,f($\frac{a}{2b}$)=1,
∴$\left\{\begin{array}{l}{a>b}\\{a=2\sqrt{b}}\end{array}\right.$,
∴a2=4b<4a,
∴0<a<4;
②$\frac{a}{b}$>1时,$\left\{\begin{array}{l}{f(\frac{a}{2b})=1}\\{f(1)≥-1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a>b}\\{{a}^{2}=4b}\\{a-b≥-1}\end{array}\right.$,
∴a2=4b<4a,
∴0<a<4,
∵b=$\frac{{a}^{2}}{4}$,
∴a-$\frac{{a}^{2}}{4}$≥-1,∴a2-4a-4≤0,
∴2-2$\sqrt{2}$≤a≤2+2$\sqrt{2}$
综上所述,0<a<4.
点评 本题考查二次函数的图象和性质,主要有开口方向,对称轴,单调性和最值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
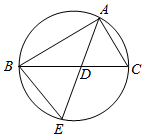 如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
如图,△ABC的角平分线AD的延长线交它的外接圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.
如图,已知三棱柱ABC-A′B′C′的所有棱长都是2,且∠A′AB=∠A′AC=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com