
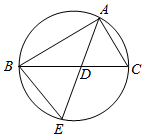
 如图,△ABC的角平分线AD的延长线交它的外接圆于点E.
如图,△ABC的角平分线AD的延长线交它的外接圆于点E.分析 (1)运用同弧所对圆周角相等与角平分线性质,构造两个三角形相似,从而证明出$\frac{AB}{AE}$=$\frac{AD}{AC}$;
(2)利用三角形的面积公式构造出等式,求出sin∠BAC的值,继而求出∠BAC的大小.
解答 解:(1)证明:∵AD是△ABC的角平分线,
∴∠BAE=∠DAC,
又$\widehat{AB}$所对的圆周角相等,即∠BEA=∠DCA.
∴在△ABE与△ACD中,
∠BAE=∠DAC,∠BEA=∠DCA,
∴△ABE∽△ADC,
∴$\frac{AB}{AE}=\frac{AD}{AC}$.
(2)由(1)知$\frac{AB}{AE}$=$\frac{AD}{AC}$,所以有AB•AC=AD•AE.
又△ABC的面积S=$\frac{1}{2}$AD•AE=$\frac{1}{2}$AB•AC=$\frac{1}{2}AB•ACsin∠BAC$.
∴$sin∠BAC=\frac{π}{2}$,故$∠BAC=\frac{π}{2}$.
点评 本题主要考查了通过两个角相等证明三角形相似的方法,通过三角形的面积公式构造成等式,求解∠BAC的大小.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,-2,4) | B. | (3,2,-4) | C. | (3,2,4) | D. | (-3,-2,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,且过点$(1,\frac{{\sqrt{3}}}{2})$.(1)求椭圆C的方程;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{{\sqrt{2}}}{2}$) | B. | ($\frac{{\sqrt{2}}}{2}$,1) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
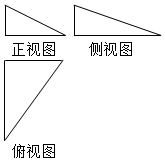 己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )
己知三棱锥的三视图如图所示,其主视图、侧视图、俯视图的面积分别为1,$\frac{3}{2}$,3,则该三棱锥的外接球体积为( )| A. | $\frac{28\sqrt{14}}{3}$π | B. | $\frac{56\sqrt{14}}{3}$π | C. | $\frac{7\sqrt{14}}{3}$π | D. | $\frac{7\sqrt{14}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>3} | B. | {x|x<0或x>2} | C. | {x|x<0或x>3} | D. | {x|x<-1或x>3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com